Electronics and Communication Engineering - Exam Questions Papers - Discussion
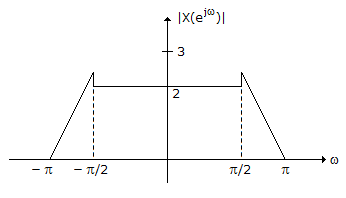
- x(n) is periodic
- Real
- Even
- Finite energy
Accordingly, we note first that periodicity in the time domain implies that the Fourier transform is zero, except possibly for impulses located at various integer multiples of the fundamental frequency.
This is not true for X(ejω). We conclude, then, that x[n] is not periodic.
Next, from the symmetry properties for Fourier Transforms, we know that a real valued sequence must have a Fourier transform of even magnitude and a phase function that is odd.
This is true for the given |X(ejω)| and ∠X(ejω). We thus conclude that x[n] is real.
Third, if x[n] is an even function, then, by the symmetry properties for real signals, X(ejω) must be real and even.
However, since X(ejω) = |X(ejω)| e-j2ω, X(ejω) is not a real-valued function.
Consequently, x[n] is not even.
Finally, to test for the finite-energy property, we may use Parseval's relation,
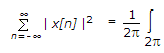 |X(ejω)|2 dω
|X(ejω)|2 dω
It is clear that integrating |X(ejω)|2 from - p to p will yield a finite quantity.
We conclude that x[n] has finite energy.