Electronics and Communication Engineering - Analog Electronics - Discussion
Discussion Forum : Analog Electronics - Section 1 (Q.No. 12)
12.
In figure, VEB = 0.6 V, β = 99. Then VC and IC are
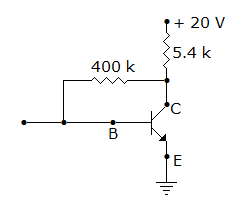

Answer: Option
Explanation:
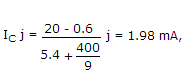
VC = 20 - 1.98 x 10-3 x 5.4 x 103  9.3 V.
9.3 V.
Discussion:
11 comments Page 1 of 2.
Nishad said:
5 years ago
We will apply for normal kvl.
First, understand that here feedback resistor is placed between collector and base to keep the transistor in active region irrespective of beta value
So current through 5.4k will be Ic+Ib. Current through 400k will be Ib.
Now apply kvl.
20 = 5.4k *(Ic+Ib) + 400k * Ib + Vbe.
Substitute Ic with beta*Ib.
We will get Ib = .02mA.
Now Ic =beta*Ib = 1.98mA.
Vc = Vcc- Rc( Ib + Ic)= 9.2V.
First, understand that here feedback resistor is placed between collector and base to keep the transistor in active region irrespective of beta value
So current through 5.4k will be Ic+Ib. Current through 400k will be Ib.
Now apply kvl.
20 = 5.4k *(Ic+Ib) + 400k * Ib + Vbe.
Substitute Ic with beta*Ib.
We will get Ib = .02mA.
Now Ic =beta*Ib = 1.98mA.
Vc = Vcc- Rc( Ib + Ic)= 9.2V.
(4)
Sandeep said:
1 decade ago
Why 400/9 is taken?
Arif said:
1 decade ago
Use these formulas:
Ib = (Vcc-Vbe)/(Rb+BRc).
Ic = BIb.
Vc = Vcc-IcRc.
Ib = (Vcc-Vbe)/(Rb+BRc).
Ic = BIb.
Vc = Vcc-IcRc.
Sivaiah said:
9 years ago
In question, they mention it as Veb but it is Vbe.
Chenelyn Cedron said:
9 years ago
@Sandeep It's 400/99, just a typo error.
In fact, if you are bookish enough and you hate approximations, your first equation might look like this:
Vcc = V{5.4k} + V{400k} + V{be}.
Vcc = ((B)(Ib) + 1)(5.4k)(Ic)/B + (400k)(Ic)/B + V{be}.
Substituting the given gives:
20 = (99 + 1)(5.4k)(Ic)/(99) + (400k)(Ic)/(99) + 0.6.
This would give you an Ic of 2.043 mA.
Then since Vce = Vc = Vcc - IcRc,
Vc = 20 - (2.043mA)(5.4k) = 8.97 V. Pretty close to letter A.
In fact, if you are bookish enough and you hate approximations, your first equation might look like this:
Vcc = V{5.4k} + V{400k} + V{be}.
Vcc = ((B)(Ib) + 1)(5.4k)(Ic)/B + (400k)(Ic)/B + V{be}.
Substituting the given gives:
20 = (99 + 1)(5.4k)(Ic)/(99) + (400k)(Ic)/(99) + 0.6.
This would give you an Ic of 2.043 mA.
Then since Vce = Vc = Vcc - IcRc,
Vc = 20 - (2.043mA)(5.4k) = 8.97 V. Pretty close to letter A.
Neeraj said:
9 years ago
Operating Vbe should be 0.7.
Prutha said:
8 years ago
I am Not clear with the solution. Please explain.
Aman said:
7 years ago
Apply kvl from 20-Ic * 5.4-Ib * 400-0.6 = 0.
You will get Ib=. 02ma.then Ic=BIb=1.98ma.
Now you can easily find Vc.
You will get Ib=. 02ma.then Ic=BIb=1.98ma.
Now you can easily find Vc.
Karthik said:
7 years ago
What is 400/9?
Vasanthakumara D said:
6 years ago
This question 400/9 how come 9?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers