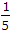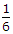Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 6)
6.
The ratio of elongations of a conical bar due to its own weight and that of a prismatic bar of the same length, is
Discussion:
18 comments Page 1 of 2.
Deepal Maheshwari said:
9 years ago
Elongation = PL/AE.
Now the weight of a bar of the conical shape is 1/3φr2h assuming both bars of the same material so neglecting density weight = volume.
And, the weight of the prismatic bar is φr2h.
So the weight of the conical bar is 1/3 to the prismatic bar.
Elongation in conical bar = PL/3AE.
Elongation in a prismatic bar = PL/AE .
Here, Ratio will be 1:3.
Now the weight of a bar of the conical shape is 1/3φr2h assuming both bars of the same material so neglecting density weight = volume.
And, the weight of the prismatic bar is φr2h.
So the weight of the conical bar is 1/3 to the prismatic bar.
Elongation in conical bar = PL/3AE.
Elongation in a prismatic bar = PL/AE .
Here, Ratio will be 1:3.
Mujru said:
9 years ago
Γ * length. Squre/2 E.
Γ = unit weight of material.
E = young modulus.
But here bar said to be conical so the 1/3 multiple the 1st equation.
So the final equation is;.
Γ * length squre/6E.
So the answer is 1/3.
Γ = unit weight of material.
E = young modulus.
But here bar said to be conical so the 1/3 multiple the 1st equation.
So the final equation is;.
Γ * length squre/6E.
So the answer is 1/3.
Baloch said:
9 years ago
Elongation of the prismatic bar due to its own weight = w l ^ 2 /2E .
Elongation of the conical bar due to its own weight = w l ^ 2 /6E.
wl^2/2E ÷ wl^2 / 6E,
wl^2/2E x 6E / wl^2,
(wl^2 and E canceled)
2/6 = 1/3.
Elongation of the conical bar due to its own weight = w l ^ 2 /6E.
wl^2/2E ÷ wl^2 / 6E,
wl^2/2E x 6E / wl^2,
(wl^2 and E canceled)
2/6 = 1/3.
Vetan said:
6 years ago
Elongation of a cylinder rod of diameter D,
Length L and wt density w.
Wl2/2E.
Elongation of a conical rod of diameter D, at support with Length L and wt density w.
Wl2/6E.
Its ratio is 1/3.
Length L and wt density w.
Wl2/2E.
Elongation of a conical rod of diameter D, at support with Length L and wt density w.
Wl2/6E.
Its ratio is 1/3.
(3)
Parth said:
5 years ago
Simple solution:
The Volume of Cone = 1/3. (π). r^2. h.
Volume of prismatic bar(always cylinder) = (π). r^2. h.
Take the ratio cone/cylinder: 1/3.
The Volume of Cone = 1/3. (π). r^2. h.
Volume of prismatic bar(always cylinder) = (π). r^2. h.
Take the ratio cone/cylinder: 1/3.
(5)
Durgesh said:
9 years ago
If length and weight of both prismatic and conical same. Then the ratio of their elongation due to their own weight will be?
Please give me the answer.
Please give me the answer.
Lakhan Bhavnani said:
7 years ago
WL^2/6AE for the conical bar.
And
WL^2/2AE for the prismatic bar.
Then ratio of the conical bar to prismatic bar is;
(WL^2/6AE)/(WL^2/2AE) = 1/3(ANS).
And
WL^2/2AE for the prismatic bar.
Then ratio of the conical bar to prismatic bar is;
(WL^2/6AE)/(WL^2/2AE) = 1/3(ANS).
Neelam shekhawat said:
1 decade ago
Elongation of a conical bar due to its own weight is = (lemma) *L^2 divided by 6AE.
Elongation of a prismatic bar is = (lemda)*L^2 divided by 2AE.
Elongation of a prismatic bar is = (lemda)*L^2 divided by 2AE.
Navjeet singh Nit patna said:
8 years ago
Because for prismatic bar =YL^2/2E.
and for conical bar =YL^2/6E.
So that ratio =YL^2/6E*2E/YL^2=1/3.
and for conical bar =YL^2/6E.
So that ratio =YL^2/6E*2E/YL^2=1/3.
Munish said:
9 years ago
Deflection due to self weight = wl/2AE.
Deflection of 2nd beam = Wl/2AE + WL/AE.
Equate and Ratio is 1:3.
Deflection of 2nd beam = Wl/2AE + WL/AE.
Equate and Ratio is 1:3.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers