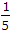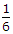Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 6)
6.
The ratio of elongations of a conical bar due to its own weight and that of a prismatic bar of the same length, is
Discussion:
18 comments Page 1 of 2.
SPG said:
4 years ago
Elongation in conical bar = AL/3AE.
Elongation in a Prismatic bar = PL/AE,
The ratio will be =1:3.
Elongation in a Prismatic bar = PL/AE,
The ratio will be =1:3.
(10)
Parth said:
5 years ago
Simple solution:
The Volume of Cone = 1/3. (π). r^2. h.
Volume of prismatic bar(always cylinder) = (π). r^2. h.
Take the ratio cone/cylinder: 1/3.
The Volume of Cone = 1/3. (π). r^2. h.
Volume of prismatic bar(always cylinder) = (π). r^2. h.
Take the ratio cone/cylinder: 1/3.
(5)
Vetan said:
6 years ago
Elongation of a cylinder rod of diameter D,
Length L and wt density w.
Wl2/2E.
Elongation of a conical rod of diameter D, at support with Length L and wt density w.
Wl2/6E.
Its ratio is 1/3.
Length L and wt density w.
Wl2/2E.
Elongation of a conical rod of diameter D, at support with Length L and wt density w.
Wl2/6E.
Its ratio is 1/3.
(3)
Monika said:
7 years ago
Y is weight density.
That is w = Y * volume.
That is w = Y * volume.
(1)
Pritish said:
8 years ago
(WL^2/6E)/(WL^2/2E) = 1/3.
(1)
Azzu said:
8 years ago
For conical bar = γ l^2/(6E).
Prismatic bar=γ l^2/(2E),
Ratio of above values =1/3.
Prismatic bar=γ l^2/(2E),
Ratio of above values =1/3.
Raj said:
4 years ago
So which bar is more elongation? Please explain.
Lakhan Bhavnani said:
7 years ago
WL^2/6AE for the conical bar.
And
WL^2/2AE for the prismatic bar.
Then ratio of the conical bar to prismatic bar is;
(WL^2/6AE)/(WL^2/2AE) = 1/3(ANS).
And
WL^2/2AE for the prismatic bar.
Then ratio of the conical bar to prismatic bar is;
(WL^2/6AE)/(WL^2/2AE) = 1/3(ANS).
Vicky said:
8 years ago
Isn't there any difference between Y (γ) and W (weight)?
Neelam shekhawat said:
1 decade ago
Elongation of a conical bar due to its own weight is = (lemma) *L^2 divided by 6AE.
Elongation of a prismatic bar is = (lemda)*L^2 divided by 2AE.
Elongation of a prismatic bar is = (lemda)*L^2 divided by 2AE.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers