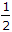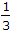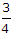Civil Engineering - Hydraulics - Discussion
Discussion Forum : Hydraulics - Section 4 (Q.No. 43)
43.
The ratio of the hydraulic radius of a pipe running full to the hydraulic radius of a square section of a channel whose side is equal to the diameter of the pipe, is
Discussion:
22 comments Page 1 of 3.
Inayat Ullah Kakar said:
1 year ago
It is very simple;
R = D/4 for circular section
And for;
In square section we know that;
R = area/ wetted perimeter
R = BD/B + 2D.
In questions that B= D because of the square section
R = D^2/3D
R =D/3
So, ratio R1/R2.
D/4÷ D/3.
We get 3/4.
So the given answer is correct.
R = D/4 for circular section
And for;
In square section we know that;
R = area/ wetted perimeter
R = BD/B + 2D.
In questions that B= D because of the square section
R = D^2/3D
R =D/3
So, ratio R1/R2.
D/4÷ D/3.
We get 3/4.
So the given answer is correct.
(3)
Timi said:
2 years ago
@All.
Option A, 1 would be correct if it was a square pipe. Here it is a channel. So three sides would be included in wetted parameters.
Option A, 1 would be correct if it was a square pipe. Here it is a channel. So three sides would be included in wetted parameters.
(1)
Jero M said:
3 years ago
According to me, it's option A.
(1)
Hemanth said:
3 years ago
Answer is 1.
In question, they are asking about hydraulic radius, not hydraulic mean depth Hydraulic radius RC.
The hydraulic diameter of circles D=4A/P RADIUS=D/2
A= √D2/4 P=√D.
For square section side D.
A=D^2 P=4D.
RATIO CIRCLES/SQUARE.
THE ANSWER IS 1.
OPTION A IS CORRECT.
In question, they are asking about hydraulic radius, not hydraulic mean depth Hydraulic radius RC.
The hydraulic diameter of circles D=4A/P RADIUS=D/2
A= √D2/4 P=√D.
For square section side D.
A=D^2 P=4D.
RATIO CIRCLES/SQUARE.
THE ANSWER IS 1.
OPTION A IS CORRECT.
(2)
Saurabh said:
4 years ago
D is the correct answer.
Hydraulic radius of circular section = D/4.
And for square = D/3,
So, the ratio is = 3/4.
Hydraulic radius of circular section = D/4.
And for square = D/3,
So, the ratio is = 3/4.
(4)
Dhiru said:
5 years ago
A is the correct option.
So, R = d/4-d/4 = 1.
So, R = d/4-d/4 = 1.
(1)
Ketema Feye said:
5 years ago
Agree, D is the correct answer.
Hasmukh parmar said:
6 years ago
The hydraulic radius of circle = d/4.
The hydraulic radius of square = d/3 ( because here we are considering wetted perimeter so two sides and bottom are wetted but top width is not wetted because it's open in the atmosphere)
So, correct answer is = d.3/d.4 = 3/4.
The hydraulic radius of square = d/3 ( because here we are considering wetted perimeter so two sides and bottom are wetted but top width is not wetted because it's open in the atmosphere)
So, correct answer is = d.3/d.4 = 3/4.
(2)
Abhik said:
7 years ago
D is correct, i.e R = A\P.
Jay said:
7 years ago
@All.
But remember the question says that the square section is running full to the wetted perimeter should be 4D and not 3D and by this, the answer should be A.
But remember the question says that the square section is running full to the wetted perimeter should be 4D and not 3D and by this, the answer should be A.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers