Non Verbal Reasoning - Analytical Reasoning - Discussion
Discussion Forum : Analytical Reasoning - Section 1 (Q.No. 1)
1.
Find the number of triangles in the given figure.

Answer: Option
Explanation:
The figure may be labelled as shown.
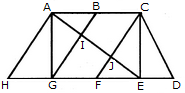
The simplest triangles are AHG, AIG, AIB, JFE, CJE and CED i.e. 6 in number.
The triangles composed of two components each are ABG, CFE, ACJ and EGI i.e. 4 in number.
The triangles composed of three components each are ACE, AGE and CFD i.e. 3 in number.
There is only one triangle i.e. AHE composed of four components.
Therefore, There are 6 + 4 + 3 + 1 = 14 triangles in the given figure.
Discussion:
55 comments Page 5 of 6.
Gajanan Konge said:
1 decade ago
@ Priyanka.
This formula doesn't work as, there is one more triangle present in the figure and it is AHE (That comprises of the four components).
This formula doesn't work as, there is one more triangle present in the figure and it is AHE (That comprises of the four components).
Srini said:
1 decade ago
@Priyanka.
What are the limitation to apply this formula,
No.of total nodes + 2(no.of inner nodes).
What are the limitation to apply this formula,
No.of total nodes + 2(no.of inner nodes).
Raghu said:
1 decade ago
Is there any shortcut to find these kind of questions?
Rajesh said:
1 decade ago
Not understanding about nodes, please explain clearly.
Madhu said:
1 decade ago
Node means point.
Sowmya said:
1 decade ago
What is meant by nodes?
Bhuvanesh said:
1 decade ago
Nodes means intersecting points.
Ali said:
1 decade ago
Can any one explain components again?
Amrish said:
1 decade ago
What is meant by node and antinode and how should we count them?
Shalini said:
1 decade ago
There is another method to solve this problem:
1. First check the possible Triangle by Assume each node or point as (A,B,C,D,E,F,G,I,J) .
2. Second check the possibility of Joining each node i.e (AHG,ABI,AGI,AGB,AEG).
3. Then check for B and see what possible joining are available i.e(BIA,BGA).
4. Again check for C (CED,CFE,CIE,CFD) D (DEC,DFC) E (ECJ,ECF) F(FJE,FCE,FCD) G (GAE,GAI,GAB,GAH) H(HAG,HAE).
5. NOW Combine all Elements.
AHG,ABI,AGI,AGB,AEG,BIA,BGA,CED,CFE,CIE,CFD,DEC,DFC,ECJ,ECF,FJE,FCE,FCD,GAE,GAI,GAB,GAH,HAG,HAE
6. Now Eliminate same letter (AHG -> HAG)i.e remove HAG.
7. If you eliminate you will get,(AHG,ABI,AGI,AGB,AEG,BGA,CED,CFE,CIE,CFD,DFC,ECJ,FJE,HAS).
TOTALLY 14 letter are remaining..
Hope you all Understand :).
1. First check the possible Triangle by Assume each node or point as (A,B,C,D,E,F,G,I,J) .
2. Second check the possibility of Joining each node i.e (AHG,ABI,AGI,AGB,AEG).
3. Then check for B and see what possible joining are available i.e(BIA,BGA).
4. Again check for C (CED,CFE,CIE,CFD) D (DEC,DFC) E (ECJ,ECF) F(FJE,FCE,FCD) G (GAE,GAI,GAB,GAH) H(HAG,HAE).
5. NOW Combine all Elements.
AHG,ABI,AGI,AGB,AEG,BIA,BGA,CED,CFE,CIE,CFD,DEC,DFC,ECJ,ECF,FJE,FCE,FCD,GAE,GAI,GAB,GAH,HAG,HAE
6. Now Eliminate same letter (AHG -> HAG)i.e remove HAG.
7. If you eliminate you will get,(AHG,ABI,AGI,AGB,AEG,BGA,CED,CFE,CIE,CFD,DFC,ECJ,FJE,HAS).
TOTALLY 14 letter are remaining..
Hope you all Understand :).
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers