Non Verbal Reasoning - Analytical Reasoning - Discussion
Discussion Forum : Analytical Reasoning - Section 1 (Q.No. 1)
1.
Find the number of triangles in the given figure.

Answer: Option
Explanation:
The figure may be labelled as shown.
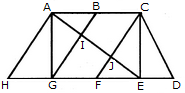
The simplest triangles are AHG, AIG, AIB, JFE, CJE and CED i.e. 6 in number.
The triangles composed of two components each are ABG, CFE, ACJ and EGI i.e. 4 in number.
The triangles composed of three components each are ACE, AGE and CFD i.e. 3 in number.
There is only one triangle i.e. AHE composed of four components.
Therefore, There are 6 + 4 + 3 + 1 = 14 triangles in the given figure.
Discussion:
55 comments Page 1 of 6.
RIDAM said:
1 month ago
Thanks everyone for explaining the answer.
Anil said:
2 months ago
Yes, Agree, Option D.
(1)
Sayali Patil said:
2 years ago
According to me, it is 12 triangles.
(9)
Saiteja said:
2 years ago
@All.
Count the triangles by considering parts separately.
For the above figure consider the middle rectangle separately and count. Then left and right triangle along with the triangle included in the rectangle, total =14.
Count the triangles by considering parts separately.
For the above figure consider the middle rectangle separately and count. Then left and right triangle along with the triangle included in the rectangle, total =14.
(3)
Shreya said:
4 years ago
I found only 9 triangles, how it is 14? Anyone explain me clearly please.
(5)
Muhammad Ibad ALi said:
4 years ago
Components mean that how many sections the triangle is divided.
(4)
Diya said:
5 years ago
Thanks @Priyanka.
(4)
Madhuri said:
7 years ago
The easiest way is to pick an edge at a time from the boundary like AH and count the no. Of triangles having it as one of its sides. These are AHG and AHE.
Then take up the next edge, say AC and count the no of triangles formed with it. These are ACE and ACJ.
Similarly, for GE the triangles are GEA and GEI.
For AG, we have AGB, AGI
For CE, we have, CEJ, CEF
For CD, it is CDE and CDF
Besides these, there are ABI, EFJ.
No more triangles are there. And the counting has reached 14.
The way to confirm that no triangles are left uncounted is to pick the edges one by one in a cyclic manner that is to start from a vertex and keep on moving from it in a certain direction along the boundary of the given figure.
Then take up the next edge, say AC and count the no of triangles formed with it. These are ACE and ACJ.
Similarly, for GE the triangles are GEA and GEI.
For AG, we have AGB, AGI
For CE, we have, CEJ, CEF
For CD, it is CDE and CDF
Besides these, there are ABI, EFJ.
No more triangles are there. And the counting has reached 14.
The way to confirm that no triangles are left uncounted is to pick the edges one by one in a cyclic manner that is to start from a vertex and keep on moving from it in a certain direction along the boundary of the given figure.
(5)
Swati said:
7 years ago
Thanks @Priyanka.
(1)
SANTHOSH said:
7 years ago
Nice shortcut, thank you @Priyanka.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers