Non Verbal Reasoning - Analytical Reasoning
- Analytical Reasoning - Section 1
- Analytical Reasoning - Section 2
Count the number of convex pentagons in the adjoining figure.
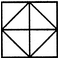
A convex pentagon has no angles pointing inwards. More precisely, no internal angles can be more than 180°.
The figure may be labelled as shown.
The pentagons in the figure, are ABDFH, CDFHB, EFHBD, GHBDF, ACDFG, CEFHA, EGHBC, GABDE, BDEGH, DFGAB, FHACD and HBCEF. Clearly, these are 12 in number.
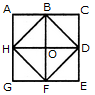
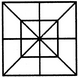
Count the number of rectangles in the given figure.
The figure may be labelled as shown.
The rectangles composed of two components each are HIJE, EKJ,F, FMNG, GPQH, AEOH, EBFO, OFCG and HOGD i.e. 8 in number.
The rectangles composed of four components each are ABFH, BCGE, CDHF, DAEG and EFGH i.e. 5 in number.
The rectangles composed of six components each are IJFG, KLGH, MNHE and PQEF i.e. 4 in number.
The rectangles composed of eight components each are IJMN, KLPQ and ABCD i.e. 3 in number.
Thus, there are 8 + 5 + 4 + 3 = 20 rectangles in the given figure.
(Here note that the squares are also counted amongst rectangles)
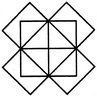
Count the number of triangles and squares in the given figure.
The figure may be labelled as shown.
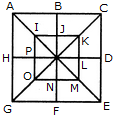
Triangles :
The simplest triangles are IJQ, JKQ, KLQ, LMQ, MNQ, NOQ, OPQ and PIQ i.e. 8 in number. The triangles composed of two components each are ABQ, BCQ, CDQ, DEQ, EFQ, FGQ, GHQ, HAQ, IKQ, KMQ, MOQ and OIQ i.e. 12 in number.
The triangles composed of four components each are ACQ, CEQ, EGQ, GAQ, IKM, KMO, MOI and OIK i.e. 8 in number.
The triangles composed of eight components each are ACE, CEG, EGA and GAC i.e. 4 in number.
Total number of triangles in the figure = 8 + 12 + 8 + 4 = 32.
Squares :
The squares composed of two components each are IJQP, JKLQ, QLMN and PQNO i.e. 4 in number.
The squares composed of four components each are ABQH, BCDQ, QDEF and HQFG i.e. 4 in number.
There is only one square i.e. IKMO composed of eight components.
There is only one square i.e. ACEG composed of sixteen components.
Thus, there are 4 + 4 + 1 + 1= 10 squares in the given figure.
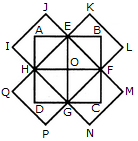
Count the number of parallelogram in the given figure.
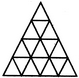
The figure may be labelled as shown.
The parallelograms composed of two components each are ADME, DFNM, EMOG, FHJN, MNKO, GOLI, HBJN, NJKO, OKLI, FHNM, MNOG, DFME, HJKN, NKLO, OLCI, FNOM, MOIG and DMGE. i.e. 18 in number.
The parallelograms composed of four components each are HOKB, NILJ, FGOH, HOLJ, NICK, FGIN, FMJB, DENH, MGKJ, MGCL, DEIO, FMLK, AENF, AGOD, DMJH, DOKF, EILM and EGKN i.e. 18 in number.
The parallelograms composed of six components each are AEJH, DAIL, DECL, DEJB, HILB and HICJ i.e. 6 in number.
The parallelograms composed of eight components each are FGKB, FGCK and AGKF i.e. 3 in number.
Total number of parallelograms in the figure = 18 + 18 + 6 + 3 = 45.
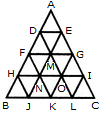
Count the number of parallelogram in the given figure.
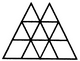
The figure may be labelled as shown.
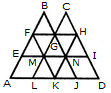
The simplest parallelograms are EMLA and NIDJ i.e. 2 in number.
The parallelograms composed of two components each are BFMG, CGNH, GMKN, FGME, GHNM, MNKL, FGNM, GHIN and MNJK i.e. 9 in number.
The parallelograms composed of three components each are FGLA, ENKA, GHDJ and MIDK ie. 4 in number.
The parallelograms composed of four components each are FGJK, GHKL, FBNK, CHKM, EFHN and MFHI i.e. 6 in number.
The parallelograms composed of seven components each are FHKA and FHDK i.e. 2 in number.
Total number of parallelograms in the figure = 2 + 9 + 4 + 6 + 2 = 23.