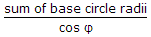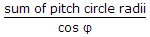Mechanical Engineering - Theory of machines - Discussion
Discussion Forum : Theory of machines - Section 1 (Q.No. 22)
22.
The centre distance between two meshing involute gears is equal to
Discussion:
5 comments Page 1 of 1.
Ganeshr said:
5 years ago
@Vinay
Let pcd of 1st gear is D1 & pcd of 2nd gear is D2.
We know that distance between the centre of gear is = (D1+D2)/2= R1+R2.
From the geometry of gear meshing.
R1 = (base circle radius if 1 )/cosφ.
R2 = (base circle radius if 2 )/cosφ.
Therefore R1+R2=sum of base circle radio/ cosφ.
Let pcd of 1st gear is D1 & pcd of 2nd gear is D2.
We know that distance between the centre of gear is = (D1+D2)/2= R1+R2.
From the geometry of gear meshing.
R1 = (base circle radius if 1 )/cosφ.
R2 = (base circle radius if 2 )/cosφ.
Therefore R1+R2=sum of base circle radio/ cosφ.
(1)
Vinay BEL said:
5 years ago
Anyone explain in detail.
Nabam said:
9 years ago
It's more like base circle diameter equal to pitch circle diameter multiplied by cos (φ).
Dayanand yadav said:
9 years ago
@Roopkanwar.
C1 and C2 are base circle radii, not the diameter.
C1 and C2 are base circle radii, not the diameter.
Roopkanwar said:
1 decade ago
It's a formula that is equal to C1+C2/cos (phi).
Where C1 and C2 are base circle diameter.
Where C1 and C2 are base circle diameter.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers