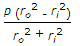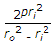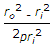Mechanical Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 9)
9.
A thick cylindrical shell having ro and ri as outer and inner radii, is subjected to an internal pressure (p). The maximum tangential stress at the inner surface of the shell is
Discussion:
20 comments Page 1 of 2.
Rajat kumar said:
6 years ago
Can explain, how the area will get?
(1)
Rohit sinha said:
7 years ago
It is similar to longitudinal stress in the thick cylinder.
σ*π(ro2-ri2)=p*area.
σ*π(ro2-ri2)=p*area.
Haftu melaku said:
7 years ago
Give me the brief explanation of the solution, please!
(1)
Kiran said:
8 years ago
Anyone, please explain it briefly.
(1)
Lavanya said:
8 years ago
Yes, stress = pressure/Area.
Area of cylindrical shell = (ri^2 - ro^2)/(ri^2+ro^2).
Hence, stress= p(ri^2+ro^2)/(ri^2-ro^2).
Area of cylindrical shell = (ri^2 - ro^2)/(ri^2+ro^2).
Hence, stress= p(ri^2+ro^2)/(ri^2-ro^2).
(12)
Rohit said:
9 years ago
Stress=pressure*Area(pressure)/Area(stress).
Area (Pressure)=π/4(ri^2+r0^2) Area (Stress)=π/4(ri^2-r0^2).
Area (Pressure)=π/4(ri^2+r0^2) Area (Stress)=π/4(ri^2-r0^2).
(1)
Sruthi said:
9 years ago
Can anyone explain the formula.
(1)
Roshan Gaykar said:
9 years ago
It is a standard formula illustrates in thin cylindrical shell chapter.
(1)
Ankit kumar said:
9 years ago
This is a standard formula also derived by R. S Khurmi book.
Mohtashim said:
9 years ago
Can anyone give its derivation, for proper understanding?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers