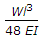Mechanical Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 25)
25.
For a beam, as shown in the below figure, when the load W is applied in the centre of the beam, the maximum deflection is


Discussion:
20 comments Page 1 of 2.
Hemlal sahu said:
1 decade ago
This question given answer option & response answer is incorrect. Above answer is simply.
Supported beam with central point load.
WWa/12.726EIl (l2-E2) 3/2.
Supported beam with central point load.
WWa/12.726EIl (l2-E2) 3/2.
Rajkotha said:
7 years ago
Simply supported beam Wl^3/48EI.
Simply supported with UDL -5WL^4/384EI.
Both ends fixed -WL^3/192EI.
Both ends fixed with UDL -WL^4/384EI.
Simply supported with UDL -5WL^4/384EI.
Both ends fixed -WL^3/192EI.
Both ends fixed with UDL -WL^4/384EI.
(5)
Shridhar Yadav said:
8 years ago
Since the load is applied Centrally.
a=b=L/2.
we have y=(w.a^2.b^2)/3EI.L putting above values in this we get,
y=(wL^3)/48EI.
a=b=L/2.
we have y=(w.a^2.b^2)/3EI.L putting above values in this we get,
y=(wL^3)/48EI.
(1)
Sanjay kumar patle said:
9 years ago
Figure is not correct, according to question force acting at the centre, its mean a = b = l/2.
wl^3/48EI = y.
wl^3/48EI = y.
Narendra Singh said:
9 years ago
The correct answer is "B".
This is simply supported beam with a load acting at the center of the beam.
This is simply supported beam with a load acting at the center of the beam.
K.rajesh said:
9 years ago
If the load acting at a distance a from one end wa/3El *(L^2-a^2/3)^3/2.
Pradeep said:
9 years ago
A is correct. Read the question carefully. Weight W is act in centre.
Ashotosh pandey said:
1 decade ago
Can be calculated simply by Macaulay's method.
RAJIV RANJAN said:
9 years ago
For the given condition y=w(a^2 *b^2)/3EIL.
Rajendra said:
8 years ago
I think 5wl^4/384EI is the correct answer.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers