Mechanical Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 6 (Q.No. 30)
30.
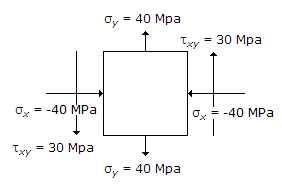
The state of stress at a point in a loaded member is shown in the below figure. The magnitude of maximum shear stress is

Discussion:
8 comments Page 1 of 1.
Shivam said:
5 years ago
Thanks for explaining @Vinod.
Alan said:
6 years ago
Apply compression sign for -40 it will become 40 so sum of 40 and 40 get 80. The easily we can get the result of 50.
Vinod said:
6 years ago
Given ,σx=-40
σy= +40
txy=+30
Formula: (1÷2)* √{(σx-σy)^2 +4txy^2}
(1÷2) * {(-40-(+40)^2 +4 * (30^2)}
Then 1÷2*(100)
Txy max=50MPA.
σy= +40
txy=+30
Formula: (1÷2)* √{(σx-σy)^2 +4txy^2}
(1÷2) * {(-40-(+40)^2 +4 * (30^2)}
Then 1÷2*(100)
Txy max=50MPA.
Numankhan said:
7 years ago
@Abhishek.
How it is txy= (30+30) =60, Please explain.
How it is txy= (30+30) =60, Please explain.
Venkat said:
7 years ago
How it is 4txy @ Abhishek. Please explain.
Abhishek said:
8 years ago
Use this equation max shear stress =1/2(√(σ^2+4txy^2))
Then put the value of σ and txy.
σ=(-40-40) =80,
txy =(30+30) =60,
Max shear stress =1/2(√(80^2 +60^2)) = 50.
Then put the value of σ and txy.
σ=(-40-40) =80,
txy =(30+30) =60,
Max shear stress =1/2(√(80^2 +60^2)) = 50.
(1)
Shobhit said:
10 years ago
Max shear stress = sqrt[{(-40- 40) / 2}^2 + 30^2].
= sqrt[40^2 + 30^2].
= sqrt(2500).
= 50 mpa.
= sqrt[40^2 + 30^2].
= sqrt(2500).
= 50 mpa.
Adithya Venkatesh said:
10 years ago
How is it 50 Mpa shouldn't it be 40 Mpa?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers