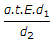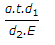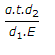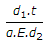Mechanical Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 3 (Q.No. 29)
29.
When a circular bar tapering uniformly from diameter d1, at one end to diameter d2 at the other end, is subjected to an increase in temperature (t), then the thermal stress induced is (where α = Coefficient of linear expansion, and E = Modulus of elasticity for the bar material)
Discussion:
5 comments Page 1 of 1.
Taral bhaumik said:
6 years ago
EαT=4PL/πd1d2E.
So load equal to P=EαTπd1d2/4L.
Take unit length so L=1.
P/A= thermal stress so divide both side by area π/4 x d2^2.
Thermal stress = EαTd1/d2.
So load equal to P=EαTπd1d2/4L.
Take unit length so L=1.
P/A= thermal stress so divide both side by area π/4 x d2^2.
Thermal stress = EαTd1/d2.
Rohan said:
8 years ago
According to me,
atE-(4Rl)/(π*d1*d2*E)=0.
So load R=atE(pi*d1*d2/4).
So stress max=atE(d1/d2).
And stress min=atE(d2/d1).
atE-(4Rl)/(π*d1*d2*E)=0.
So load R=atE(pi*d1*d2/4).
So stress max=atE(d1/d2).
And stress min=atE(d2/d1).
Maverick said:
5 years ago
Stress/strain = E so answer should have E in numerator.
Jatinder Kr. Prajapati said:
8 years ago
How it is. Can anyone explain it? Please
Sathish said:
8 years ago
Anyone explain this please.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers