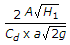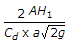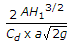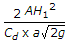Mechanical Engineering - Hydraulics and Fluid Mechanics - Discussion
Discussion Forum : Hydraulics and Fluid Mechanics - Section 1 (Q.No. 37)
37.
A tank of uniform cross-sectional area (A) containing liquid upto height (H1) has an orifice of cross-sectional area (a) at its bottom. The time required to empty the tank completely will be
Discussion:
6 comments Page 1 of 1.
Ayush said:
6 years ago
Let at time t height of water in container is h and after time dt, dh height of water flows out. At this postition dQ/dt = sqrt(2gh)*a.
A*dh=sqrt(2gh)*a*dt.
Integrating this with lower limit 0 and higher limit H we will get the answer.
A*dh=sqrt(2gh)*a*dt.
Integrating this with lower limit 0 and higher limit H we will get the answer.
(1)
DN BHASKAR said:
8 years ago
Right @Ashutosh.
Niladri Shree Chandan said:
9 years ago
Q = a * Velocity = A * (dh/dt).
=> a * (2gh)^0.5 = A * (dh/dt).
=> a * (2g)^0.5 * dt = A * (dh/(h^0.5)).
Integrating above gives the result.
=> a * (2gh)^0.5 = A * (dh/dt).
=> a * (2g)^0.5 * dt = A * (dh/(h^0.5)).
Integrating above gives the result.
Ashutosh gupta said:
10 years ago
Because the above formula is applicable for a particular height say H1.
As the water level decreases speed of flow will also decrease from max to minimum (zero) hence the average.
As the water level decreases speed of flow will also decrease from max to minimum (zero) hence the average.
HEERA LAL CHOUDHARY said:
10 years ago
Why is there extra 2?
Nihal said:
1 decade ago
It should be.
Volume/(Discharge).
= AH/(Cd*a*(2gH)^.5).
= (A*(H)^.5)/(Cd*a*(2g)^.5).
Why is there an extra 2 in the numerator?
Volume/(Discharge).
= AH/(Cd*a*(2gH)^.5).
= (A*(H)^.5)/(Cd*a*(2g)^.5).
Why is there an extra 2 in the numerator?
(1)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers