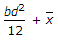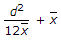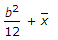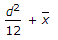Mechanical Engineering - Hydraulics and Fluid Mechanics - Discussion
Discussion Forum : Hydraulics and Fluid Mechanics - Section 2 (Q.No. 20)
20.
A vertically immersed surface is shown in the below figure. The distance of its centre of pressure from the water surface is


Discussion:
10 comments Page 1 of 1.
Gaurav Pandey said:
10 years ago
H = (I/ax) + x.....(1).
Where, I = bd^3/12.
A = b.d.
After putting the value in equation 1.
H = (bd^3/12.B.D.X) = x.
If bd is cancel out then we got:
H = d^2/12.x+x.
Where, I = bd^3/12.
A = b.d.
After putting the value in equation 1.
H = (bd^3/12.B.D.X) = x.
If bd is cancel out then we got:
H = d^2/12.x+x.
Amit said:
9 years ago
Centre heights pressure of fluid given by h#=I/Ax+x l =mol, x=distance from free surface liquid, A is area.
Amiq Syed said:
7 years ago
H=Ig/ax + x.
Ig M.I. for rectangle bd^3/12.
PpAnd area of rectangle=bd.
Solving it we get d^2/12x +x.
Ig M.I. for rectangle bd^3/12.
PpAnd area of rectangle=bd.
Solving it we get d^2/12x +x.
Nilesh Roy said:
5 years ago
Centre pressure=(Ig/A)+x.
Where Ig=moment of inertia,
A=Area.
X=From centre distance.
Where Ig=moment of inertia,
A=Area.
X=From centre distance.
Abhinav sharma said:
1 decade ago
h* = (inertia/(Ax)) + x,
where inertia is b*d^3/12 and area is A = b*d.
where inertia is b*d^3/12 and area is A = b*d.
Royal bhatia said:
1 decade ago
h = (bd^3/b.d.X)X.
After canceling out B and D we will get the answer.
After canceling out B and D we will get the answer.
Sandeep Chary said:
1 decade ago
H* = I/(A*x)+x.
I - Inertia-rectangular.
So bd^3|12.
A-area-bd.
I - Inertia-rectangular.
So bd^3|12.
A-area-bd.
Pragnan said:
1 decade ago
@Royal Batia.
Why should we divide BD^3 with B.D.X?
Why should we divide BD^3 with B.D.X?
Vishu said:
7 years ago
Height of centre of pressure = Ig/ A * x + x.
Muji said:
1 decade ago
Kindly explain me?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers