Mechanical Engineering - Engineering Mechanics - Discussion
Discussion Forum : Engineering Mechanics - Section 7 (Q.No. 10)
10.
The force induced in the string BC due to the load W as shown in the below figure is
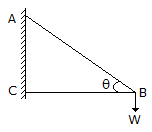

Discussion:
8 comments Page 1 of 1.
MD MOSHAHID HUSSAIN said:
7 years ago
Apply Lami's theorem,
W/Sinθ=BC/(Sin270θ)
W/Sinθ=BC/(-Cosθ)
So, BC=-WCotθ.
W/Sinθ=BC/(Sin270θ)
W/Sinθ=BC/(-Cosθ)
So, BC=-WCotθ.
Suresh s said:
7 years ago
For Equilibrium Condition Sum of horizontal forces = 0 and sum of vertical force = 0,
F @ac sin(θ) = W
F @ ac = W/ sin(θ)
And
F @ bc = F@ac cos(θ) =w cos(θ)/sin(θ)
= Wcot(θ).
F @ac sin(θ) = W
F @ ac = W/ sin(θ)
And
F @ bc = F@ac cos(θ) =w cos(θ)/sin(θ)
= Wcot(θ).
Saurabh said:
8 years ago
Thanks for the good answer @Venkat.
Saurabh said:
8 years ago
Thanks for the good answer @Venkat.
Nishant yadav said:
9 years ago
You are right and thanks @Gajendra.
Venkat said:
1 decade ago
Note: In triangle, sum of all angles is 180.
Let angle at A is a and force on CB is A. So angle A = (180 - 90 - theta) = (90 - theta).
W/sin (theta) = A/sin (90 - theta).
A = W (cos (theta)/sin (theta)) = W cot (theta).
Let angle at A is a and force on CB is A. So angle A = (180 - 90 - theta) = (90 - theta).
W/sin (theta) = A/sin (90 - theta).
A = W (cos (theta)/sin (theta)) = W cot (theta).
(2)
SAGAR said:
1 decade ago
In AB is equal to Wcosec@.
Gajendra said:
1 decade ago
w/sin@ = BC/Sin(270-@).
BC = W*(-Cos@)/Sin@.
BC = -W*Cot@.
BC = W*(-Cos@)/Sin@.
BC = -W*Cot@.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers