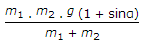Mechanical Engineering - Engineering Mechanics - Discussion
Discussion Forum : Engineering Mechanics - Section 2 (Q.No. 19)
19.
A block of mass m1, placed on an inclined smooth plane is connected by a light string passing over a smooth pulley to mass m2, which moves vertically downwards as shown in the below figure. The tension in the string is


Discussion:
13 comments Page 1 of 2.
Freind said:
5 years ago
For mass m2 : m2g-T=m2a ------> 1.
For mass m1 : T-m1gsinx=m2a -----> 2.
Find out acceleration first, then put 'a' in any one of the equation then you will get it.
For mass m1 : T-m1gsinx=m2a -----> 2.
Find out acceleration first, then put 'a' in any one of the equation then you will get it.
(2)
Prashanth said:
6 years ago
Solution;
(m1+m2)a=m2g-m1gsinα.
a=(m2g-m1gsinα)/ (m1+m2) --------> (eq1).
T-m1gsinα=m1a.
T=m1a+m1gsinα.
T=m1(a+gsinα) --------> (eq2)
Substitute eq1 in ( eq2).
T=[m1.g.m2(1.sinα)]/(m1+m2).
(m1+m2)a=m2g-m1gsinα.
a=(m2g-m1gsinα)/ (m1+m2) --------> (eq1).
T-m1gsinα=m1a.
T=m1a+m1gsinα.
T=m1(a+gsinα) --------> (eq2)
Substitute eq1 in ( eq2).
T=[m1.g.m2(1.sinα)]/(m1+m2).
Kaushal said:
6 years ago
How! Can we see derivative?
Ram said:
7 years ago
Please explain.
Chittaranjan Mahananda said:
9 years ago
Nice. Thank you all.
Satar said:
9 years ago
According to the 2nd law of newton,
For all the system;
f(net)=(m1+m2)a=m2g-m1gsin&alpa;
a=(m2g-m1gsin@)/(m1+m2).
For the mass no.2 from the free body,
F(net)=m2a.
m2-T=m2(m2g-m1gsin@)/(m1+m2).
For all the system;
f(net)=(m1+m2)a=m2g-m1gsin&alpa;
a=(m2g-m1gsin@)/(m1+m2).
For the mass no.2 from the free body,
F(net)=m2a.
m2-T=m2(m2g-m1gsin@)/(m1+m2).
Zaahir said:
9 years ago
To get accelaration you all can directly apply F = ma to total system. Then you can consider one system to get the tension as well.
Mohamed Irfan said:
9 years ago
Say it move with acceleration a then using the newtons law,
F = ma.
for mass m1 : m2g-T=m2a ------> 1.
for mass m1 : T-m1gsinx=m2a -----> 2.
If you solve this above equitation you will get T.
F = ma.
for mass m1 : m2g-T=m2a ------> 1.
for mass m1 : T-m1gsinx=m2a -----> 2.
If you solve this above equitation you will get T.
Benny said:
9 years ago
What is g?
Describe the answer.
Describe the answer.
Sunil said:
9 years ago
I don't understand. Please, anyone solve this problem.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers