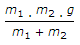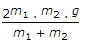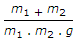Mechanical Engineering - Engineering Mechanics - Discussion
Discussion Forum : Engineering Mechanics - Section 3 (Q.No. 19)
19.
In the shown figure, the tension (T) in the string will be


Discussion:
2 comments Page 1 of 1.
Dews said:
5 years ago
Thank you @Venugopalan Cv.
Venugopalan CV said:
1 decade ago
Assume m1 > m2. Therefore, m1 will move downwards.
Net force on the system = m1.g-m2.g.
This force will cause acceleration of both the masses ie. m1+m2.
Acceleration a = (m1- m2).g/(m1+m2).
Inertia force on m1 due to this acceleration and acting upward = m1.a.
= m1(m1.g-m2.g)/(m1+m2).
Therefore net force on the string = m1.g - m1.a.
= m1.g - m1(m1-m2).g/(m1+m2).
= [m1.g(m1+m2) - m1.m1.g + m1.m2.g]/(m1+m2).
i.e. Tension in the string = 2.m1.m2.g/(m1+m2).
Net force on the system = m1.g-m2.g.
This force will cause acceleration of both the masses ie. m1+m2.
Acceleration a = (m1- m2).g/(m1+m2).
Inertia force on m1 due to this acceleration and acting upward = m1.a.
= m1(m1.g-m2.g)/(m1+m2).
Therefore net force on the string = m1.g - m1.a.
= m1.g - m1(m1-m2).g/(m1+m2).
= [m1.g(m1+m2) - m1.m1.g + m1.m2.g]/(m1+m2).
i.e. Tension in the string = 2.m1.m2.g/(m1+m2).
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers