Mechanical Engineering - Engineering Mechanics - Discussion
Discussion Forum : Engineering Mechanics - Section 6 (Q.No. 23)
23.
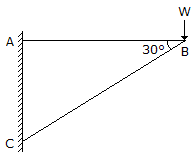
In a framed structure, as shown in the below figure, the forces in the members AB and BC are respectively

Discussion:
5 comments Page 1 of 1.
Rahul Thakur said:
5 years ago
Tan30° =w/CD = 1/√3 = CD = √3W.
Cos30 = CD/BC = √3/2= √3W/BC .
So, BC=2W.
Cos30 = CD/BC = √3/2= √3W/BC .
So, BC=2W.
(1)
GAURAV said:
6 years ago
I got another answer, can anyone explain?
(2)
KRUNAL PRAJAPATI said:
9 years ago
Full Solution:
--AB/sin(360-(90+30)) = BC/sin(90) = W/sin(30).
--AB/sin(240) = BC/sin(90)= W/sin(30).
--AB/sin(180+(90-30)) = BC/sin(90)= W/sin(30).
--AB/[-sin(90-30)] = BC/sin(90)= W/sin(30).
--AB/[-cos(30)] = BC/sin(90)= W/sin(30).
--2AB/(root3) = BC = 2W.
So, the ans is AB=(root3) * W & BC=2W.
--AB/sin(360-(90+30)) = BC/sin(90) = W/sin(30).
--AB/sin(240) = BC/sin(90)= W/sin(30).
--AB/sin(180+(90-30)) = BC/sin(90)= W/sin(30).
--AB/[-sin(90-30)] = BC/sin(90)= W/sin(30).
--AB/[-cos(30)] = BC/sin(90)= W/sin(30).
--2AB/(root3) = BC = 2W.
So, the ans is AB=(root3) * W & BC=2W.
GVR Murty said:
1 decade ago
Answer: Fab=W, Fbc=-2W;
Equation: Fab/Sin240=Fbc/Sin90=-W/Sin30.
Equation: Fab/Sin240=Fbc/Sin90=-W/Sin30.
Mbkavad said:
1 decade ago
Sin rule ab w*(sin60/sin30) = root 3. Similar to Wac.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers
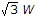 (tensile) and 2W (compressive)
(tensile) and 2W (compressive)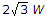 (tensile) and
(tensile) and