Engineering Mechanics - PKRB: Work and Energy - Discussion
Discussion Forum : PKRB: Work and Energy - General Questions (Q.No. 4)
4.
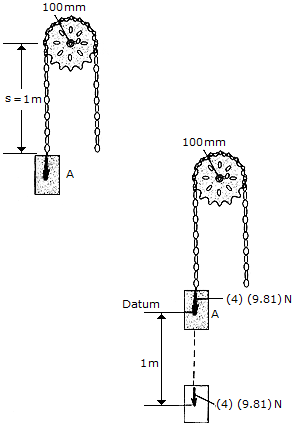
A chain that has a negligible mass is draped over a sprocket which has a mass of 2 kg and a radius of gyration of kO = 50 mm. If the 4-kg block A is released from rest in the position shown, s = 1 m, determine the angular velocity which the chain imparts th the sprocket when s = 2 m.
= 44.3 rad/s = 39.6 rad/s = 41.8 rad/s = 59.1 rad/sDiscussion:
4 comments Page 1 of 1.
Mohd Farihsan Bin Zamzuri said:
5 years ago
If the angular velocity is too high at the instant s= 2m, revise the set up to reduce the angular velocity without changing the mass of block A.
Ivan said:
8 years ago
T2= 1/2mv^2+1/2Iw^2,
= 1/2(4)(w*0.1)^2+1/2(0.005)w^2,
= 0.0225w^2.
T1+V1=T2+V2.
0+0=0.0225w^2-39.24N.
w=41.76 rad/s.
= 1/2(4)(w*0.1)^2+1/2(0.005)w^2,
= 0.0225w^2.
T1+V1=T2+V2.
0+0=0.0225w^2-39.24N.
w=41.76 rad/s.
Gege said:
8 years ago
T2= 1/2mv^2+1/2Iw^2,
= 1/2(4)(wr)^2+1/2(0.01)w^2,
= 0.01w^2.
T1+V1= T2+V2.
0+ 19.62N = 0.01w^2 + 0.
w = 44.29 rad/s.
= 1/2(4)(wr)^2+1/2(0.01)w^2,
= 0.01w^2.
T1+V1= T2+V2.
0+ 19.62N = 0.01w^2 + 0.
w = 44.29 rad/s.
Paul said:
1 decade ago
I am not sure if I am missing something with this question. I use the potential energy from the mass to determine the kinetic energy imparted on the sprocket. I use 4kg for the potential energy and then use 2 kg for the kinetic energy imparted on the sprocket.
From there I get a velocity and simply divide by the radius of 0.05 m to find the angular velocity but I don't get answer C.
From there I get a velocity and simply divide by the radius of 0.05 m to find the angular velocity but I don't get answer C.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers