Engineering Mechanics - PKRB: Force and Animation - Discussion
Discussion Forum : PKRB: Force and Animation - General Questions (Q.No. 1)
1.

The slender 200-kg beam is suspended by a cable at its end as shown. If a man pushes on its other end with a horizontal force of 30 N, determine the initial acceleration of its mass center G, the beam's angular acceleration, and the tension in the cable AB.
Discussion:
1 comments Page 1 of 1.
Amadu kwabena said:
7 years ago
How? Explain the answer in detail.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers
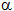 = 0.225 rad/s2, T = 1.962 kN
= 0.225 rad/s2, T = 1.962 kN