Engineering Mechanics - Force Vectors - Discussion
Discussion Forum : Force Vectors - General Questions (Q.No. 6)
6.
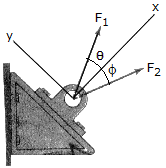
If F1 = F2 = 30lb, determine the angles 
and 
so that the resultant force is directed along the positive x axis and has a magnitude of FR = 20 lb.
= = 70.5° = = 41.4° = = 19.47° = = 18.43°Discussion:
10 comments Page 1 of 1.
Gsoutom said:
6 years ago
20^2=π30^2+30^2+2*30*30cos(2a).
2a=cos^-1(-778).
a=70.52.
2a=cos^-1(-778).
a=70.52.
Avinash Hangande said:
7 years ago
It may be possible to solve this problem using Parallelogram Method cause in answer both θ and πare same,
R= √(P^2 + Q^2 +2P*Q*Cos(α))
and
Cos(α) = (R^2 - P^2 - Q^2)/(2*P*Q)
= (20^2 - 30^2 - 30^2)/(2*30*30)
= -0.778.
α = Cos ^-1(-0.778).
α = 141.06 °
As α =π+ θ = 2θ or 2π
Since in answer it is mention that both are equal.
θ = α/ 2,
= 141.06 / 2,
= 70.52°
R= √(P^2 + Q^2 +2P*Q*Cos(α))
and
Cos(α) = (R^2 - P^2 - Q^2)/(2*P*Q)
= (20^2 - 30^2 - 30^2)/(2*30*30)
= -0.778.
α = Cos ^-1(-0.778).
α = 141.06 °
As α =π+ θ = 2θ or 2π
Since in answer it is mention that both are equal.
θ = α/ 2,
= 141.06 / 2,
= 70.52°
Yaman said:
8 years ago
Summation fx=30cos(θ)+30cos(Π)
summation fy=0
since f1=f2, then theta= Π
fx=30cos(θ)+30cos(θ)
fx=60cos(θ)
resultant=√(fx2+fy2)
20=√(3600cos2θ)
θ=70.52.
summation fy=0
since f1=f2, then theta= Π
fx=30cos(θ)+30cos(θ)
fx=60cos(θ)
resultant=√(fx2+fy2)
20=√(3600cos2θ)
θ=70.52.
Goku said:
8 years ago
Lami's theorem suits well. Consider this as 3 force system.
Daniel said:
9 years ago
Not able to understand this.
Can anyone give other methods?
Can anyone give other methods?
Ankush said:
10 years ago
No meaningful answer. Please give another solution.
Sudipta jana said:
1 decade ago
Resolving to force f1 and f2 in x and y direction, let ange pi=a and theta=b.
We get total force along x axis,
f1cosa +f2cosb.......(1).
Here the components of force f1 and f2 along y axis is opposite,and only when the component of force f1 and f2 in y direction is equal then the resultant force will be in x direction.
So f1sinb = f2sina....(2).
By solving a=band (f1 + f2)cosa=20;
cosa=cosb=20/60 So, a=b=70.52877.
We get total force along x axis,
f1cosa +f2cosb.......(1).
Here the components of force f1 and f2 along y axis is opposite,and only when the component of force f1 and f2 in y direction is equal then the resultant force will be in x direction.
So f1sinb = f2sina....(2).
By solving a=band (f1 + f2)cosa=20;
cosa=cosb=20/60 So, a=b=70.52877.
Sarah said:
1 decade ago
Note F1=F2
pi=theta so i assigned variable a to represent pi=theta
forces components in x axis components in y axis
F1=30 30 cos a 30 sin a
F2=30 + 30 cos a -30 sin a
-------------------- --------------------
Fr= 20 60 cos a 0
20=60cos a
20/60= cos a
1/3=cos a
arc cos(1/3)=a
a=70.52877937 = pi =theta
pi=theta so i assigned variable a to represent pi=theta
forces components in x axis components in y axis
F1=30 30 cos a 30 sin a
F2=30 + 30 cos a -30 sin a
-------------------- --------------------
Fr= 20 60 cos a 0
20=60cos a
20/60= cos a
1/3=cos a
arc cos(1/3)=a
a=70.52877937 = pi =theta
Mahendra singh sisodia said:
1 decade ago
Using lami's theorem
30/sin(theta)=30/sin(pi)
theta = pi
20/sin(theta+pi)=30/sin(pi)
20/sn(2pi)=30/sin(pi)
pi=70.528=theta
30/sin(theta)=30/sin(pi)
theta = pi
20/sin(theta+pi)=30/sin(pi)
20/sn(2pi)=30/sin(pi)
pi=70.528=theta
Sunil said:
1 decade ago
I want to know the steps to solve this problem...
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers