IndiaBIX

Engineering Mechanics - Equilibrium of a Rigid Body

Exercise : Equilibrium of a Rigid Body - General Questions
  • Equilibrium of a Rigid Body - General Questions
6.

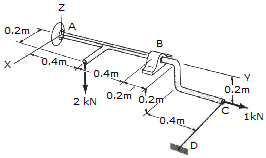
There is a ball and socket connection at A. At point B there is a connection that opposes motion in the x and z directions only. Determine the unknown force components at A and B. Use a scalar analysis.

Ax = 5.5 kN, Ay = -1.0 kN, Az = 2.75 kN, Bx = 3.5 kN, Bz = 1.25 kN, FDC = 2.0 kN
Ax = 1.5 kN, Ay = -1.0 kN, Az = 0.75 kN, Bx = -3.5 kN, Bz = 1.25 kN, FDC = 2.0 kN
Ax = 5.5 kN, Ay = -1.0 kN, Az = 2.75 kN, Bx = 3.5 kN, Bz = -0.75 kN, FDC = 2.0 kN
Ax = 1.5 kN, Ay = -1.0 kN, Az = 1.25 kN, Bx = -3.5 kN, Bz = 0.75 kN, FDC = 2.0 kN
Answer: Option
Explanation:
No answer description is available. Let's discuss.
7.

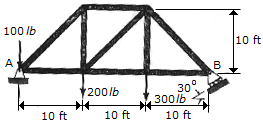
Determine the horizontal and vertical components of reaction at the pin A and the reaction at the roller support B required for equilibrium of the truss.

Ax = 0, Ay = 333 lb, NB = 267 lb
Ax = 462 lb, Ay = 66.7 lb, NB = 533 lb
Ax = 267 lb, Ay = 223 lb, NB = 377 lb
Ax = 154.0 lb, Ay = 333 lb, NB = 308 lb
Answer: Option
Explanation:
No answer description is available. Let's discuss.
8.

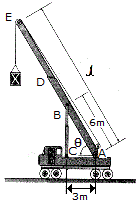
The crane provides a long-reach capacity by using the telescopic boom segment DE. The entire boom is supported by a pin at A and by the telescopic hydraulic cylinder BC, which can be considered as a two-force member. The rated load capacity of the crane is measured by a maximum force developed in the hydraulic cylinder. If this maximum force is developed when the boom supports a mass m = 6 Mg and its length is l = 40 and = 60°, determine the greatest mass that can be supported when the boom length is extended to l = 50 m and = 45°. Neglect the weight of the boom and the size of the pulley at E. Assume the crane does not overturn. Note: when = 60° BC is vertical; however, when = 45° this is not the case.

m = 7.50 Mg
m = 4.80 Mg
m = 3.26 Mg
m = 4.61 Mg
Answer: Option
Explanation:
No answer description is available. Let's discuss.
9.

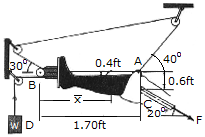
A Russell's traction is used for immobilizing femoral fractures C. If the lower leg has a weight of 8 lb, determine the weight W that must be suspended at D in order for the leg to be held in the position shown. Also, what is the tension force F in the femur and the distance 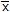which locates the center of gravity G of the lower leg? Neglect the size of the pulley at B.

x = 1.44 ft, w = 10.8 lb, F = 12.61 lb
x = 1.33 ft, w = 15.76 lb, F = 20.0 lb
x = 1.56 ft, w = 9.75 lb, F = 12.69 lb
x = 0.869 ft, w = 6.44 lb, F = 5.03 lb
Answer: Option
Explanation:
No answer description is available. Let's discuss.
10.

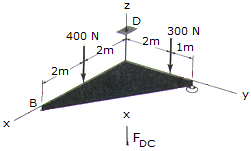
There is a ball and socket connection at A. At B there is a roller that prevents motion in the —z direction. Corner C is tied to D by a rope. The triangle is weightless. Determine the unknown force components acting at A, B, and C. Use a scalar analysis.

Ax = 0, Ay = 0, Az = 267 N, Bz = 150 N, FDC = 283 N
Ax = 0, Ay = 0, Az = 450 N, Bz = 800 N, FDC = 550 N
Ax = 0, Ay = 0, Az = 200 N, Bz = 200 N, FDC = 300 N
Ax = 0, Ay = 0, Az = 467 N, Bz = 350 N, FDC = 117.1 N
Answer: Option
Explanation:
No answer description is available. Let's discuss.
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers