Engineering Mechanics - Center of Gravity and Centroid - Discussion
Discussion Forum : Center of Gravity and Centroid - General Questions (Q.No. 5)
5.
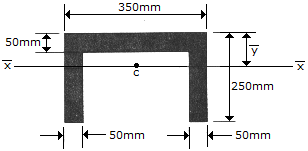
Determine the distance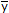 
to the centroidal axis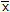 
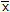of the beam's cross-sectional area.
= 112.3 mm = 125.0 mm = 100.0 mm = 91.7 mmDiscussion:
7 comments Page 1 of 1.
Rahul said:
3 years ago
Thank you everyone for explaining.
Upasana said:
7 years ago
Please, solve the question clearly.
Ali j. said:
8 years ago
Good, Thanks @Ahamed.
Ali said:
9 years ago
Please solve the question clearly by parts.
(1)
Sai lakshmi said:
10 years ago
Why didn't you do division for y2?
Danica said:
10 years ago
Why does y1 didn't consider the 350?
Ahamed said:
1 decade ago
Since the given figure is symmetric about y-axis
So therefore
x' = 0 and y' = (A1y1 + A2y2 + A3y3) / ( A1 + A2 +A3)
A1 = 350 X 50 = 17500 mm
A2 = 200 X 50 = 10000 mm
A3 = 200 X 50 = 10000 mm
y1 = 25
y2 = 50+100 = 150
y3 = 50+100 = 150
y' = (17500x25 + 10000x150 + 10000x150) / (17500 + 10000 + 10000)
y' = 91.6666666 mm
By rounding off we get,
y' = 91.7 mm.
So therefore
x' = 0 and y' = (A1y1 + A2y2 + A3y3) / ( A1 + A2 +A3)
A1 = 350 X 50 = 17500 mm
A2 = 200 X 50 = 10000 mm
A3 = 200 X 50 = 10000 mm
y1 = 25
y2 = 50+100 = 150
y3 = 50+100 = 150
y' = (17500x25 + 10000x150 + 10000x150) / (17500 + 10000 + 10000)
y' = 91.6666666 mm
By rounding off we get,
y' = 91.7 mm.
(1)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers