Electronics - Capacitors - Discussion
Discussion Forum : Capacitors - General Questions (Q.No. 35)
35.
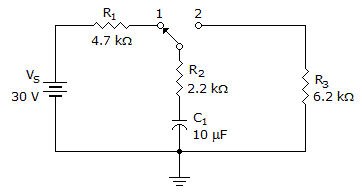
How long would it take the capacitor in the given circuit to completely discharge if the switch was in position 2?
Discussion:
18 comments Page 1 of 2.
YASHAWANTH M said:
7 years ago
Why you multiple with 5 times?
Lex said:
8 years ago
@All.
In the circuit, R2 and R3 are in kilo ohms. That's why there is *1000.
In the circuit, R2 and R3 are in kilo ohms. That's why there is *1000.
Girish kulkarni said:
8 years ago
Why here resistance added, here in fig resistance are connected in parallel know then? Please explain.
Decim said:
8 years ago
@Manikandaan and @Shadan
That 1000 is for the computation of total resistance,
(6.2+2.2)*1000= 8400 &Ohm;
That 1000 is for the computation of total resistance,
(6.2+2.2)*1000= 8400 &Ohm;
Manikandan said:
8 years ago
Why Mulitply of 1000 here?
Shadan said:
8 years ago
Why we multiply by 1000?
Naveen G said:
9 years ago
@Kiran and @Hima.
You guys substituted C = 1x10^-6 F, instead 10x10^-6 F(As given in the question).
So your answer is 42 ms (wrong), instead 420 ms (Correct).
You guys substituted C = 1x10^-6 F, instead 10x10^-6 F(As given in the question).
So your answer is 42 ms (wrong), instead 420 ms (Correct).
Hima said:
9 years ago
RC = (6.2 + 2.2) * 1000 * 10^-6 is equal to 8.4ms.
Then to completely discharge 5 time constants.
= 5RC.
= 8.4 * 5 = 42 ms.
So I agree with you @ Kiran.
Then to completely discharge 5 time constants.
= 5RC.
= 8.4 * 5 = 42 ms.
So I agree with you @ Kiran.
KIRAN V said:
9 years ago
Time constant = RC.
= (6.2 + 2.2) * 1000 * 10^-6.
= 8.4 ms.
To completely discharge 5 time constants.
= 5RC.
= 8.4 * 5 = 42 ms.
= (6.2 + 2.2) * 1000 * 10^-6.
= 8.4 ms.
To completely discharge 5 time constants.
= 5RC.
= 8.4 * 5 = 42 ms.
Abhiee said:
1 decade ago
Vc = vin*(1-e^(-t/rc)).
If we substitute t=1 rc then output of capacitor is 63.7%. Similarly if we substitute t=5*r*c in the equation. Then the output of the capacitor is 99.8%. i.e. it is fully charged.
If we substitute t=1 rc then output of capacitor is 63.7%. Similarly if we substitute t=5*r*c in the equation. Then the output of the capacitor is 99.8%. i.e. it is fully charged.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers