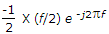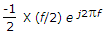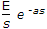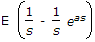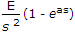IndiaBIX

Electronics and Communication Engineering - Signals and Systems

Exercise : Signals and Systems - Section 1
16.
Let x(t) and y(t) with F.T. x(f) and y(f) respectively be related as shown in figure

Then y(f) is
-X(f/2)ej2pf
-X(f/2)e- j2pf
Answer: Option
Explanation:

By applying time shifting and scaling property.

17.
Which one is a linear system?
y[n] = x[n] x x[n - 1]
y[n] = x[n] + x[n - 10]
y[n] = x2[n]
(a) and (c)
Answer: Option
Explanation:

For linearity

y1[n] = x1[n] + x2[n - 10] ...(1)

y2 = x2[n] + x2[n - 10] ...(2)

y1[n] = x1[n] + x2[n] + x2[n - 10] + x2[n - 10] ...(3)

Now find y1[n] + y2[n]

Corresponding to x1[n] + x2[n]

It is same as equation (3) hence linear.

But in part (c) y[n] = x2[n]

⇒ y1[n] = x21[n], y2[n] = x22[n]⇒ y1[n] + y2[n] = x22[n]...3

But y1[n] + y2[n]

Corresponing x1[n] + x2[n] is y1[n] + y2[n] = {x1[n] + x2[n]}2

= x12[n] + x22[n] + 2x1[n] x2[n]....4

Equations (3) and (4) are not same hence not linear.

18.
Laplace transform of a pulse function of magnitude E and duration from t = 0 to t = a is
E / s
Answer: Option
Explanation:

.

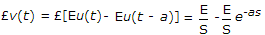19.
The continuous time system with impulse response h(t) = is stable, for n is even, when
a = 0
a > 0
a < 0
a ≤ 0
Answer: Option
Explanation:

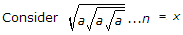
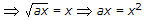
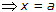
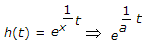
For stable system exponential must be -ve so that a < 0.

20.
If I (s) , initial value of i(t) is
5A
12.5 A
0.05 A
1250 A
Answer: Option
Explanation:

.

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers