Electronics and Communication Engineering - Networks Analysis and Synthesis - Discussion
Discussion Forum : Networks Analysis and Synthesis - Section 24 (Q.No. 48)
48.
In the transformer shown in figure, the inductance measured across terminal 1 and 2 was 4 H with terminals 3 and 4 open. It was 3H when terminals 3 and 4 are short circuited. The coefficient of coupling is
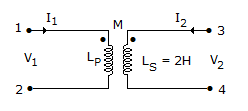
Discussion:
3 comments Page 1 of 1.
Abhirami said:
4 years ago
1st case. Open circuit 3&4.
Since terminals of the secondary are open, no current flows through the secondary.
Hence,
V1 = Lp di1/dt,
Usually, V1 = Leq di1/dt,
From the qn, Leq = 4.
Comparing the above two, we get Lp = 4.
2nd case short circuit 3&4. Current flows out of the coil and V2 = 0,
V1 = Lp di1/dt - Mdi2/dt ---> eq2.
Lsdi2/dt - Mdi1/dt,
di2/dt = (M/Ls)di1/dt ---> eq 3.
Put eq 3 in eq 2.
V1 = Lp di1/dt - M(M/Ls)di1/dt,
V1 = ( Lp - (M*M /Ls)) di1/dt ---> eq 4.
But V1 = Leq di1/dt.
Here Leq =3(from qn).
Therefore, 3 = Lp - (M*M)/Ls.
Lp = 4(deducted earlier) and Ls = 2 ( from qn),
On substitution,
3 = 4 -(M*M)/2,
6 = 8-(M*M).
M*M = 2.
From the eqn of coupling coefficient,
K^2 = M^2 / (L1*L2),
K^2 = 2/ (4*2),
K^2 = 1/4,
K = 1/2 .
K= 0.5 (Answer).
Since terminals of the secondary are open, no current flows through the secondary.
Hence,
V1 = Lp di1/dt,
Usually, V1 = Leq di1/dt,
From the qn, Leq = 4.
Comparing the above two, we get Lp = 4.
2nd case short circuit 3&4. Current flows out of the coil and V2 = 0,
V1 = Lp di1/dt - Mdi2/dt ---> eq2.
Lsdi2/dt - Mdi1/dt,
di2/dt = (M/Ls)di1/dt ---> eq 3.
Put eq 3 in eq 2.
V1 = Lp di1/dt - M(M/Ls)di1/dt,
V1 = ( Lp - (M*M /Ls)) di1/dt ---> eq 4.
But V1 = Leq di1/dt.
Here Leq =3(from qn).
Therefore, 3 = Lp - (M*M)/Ls.
Lp = 4(deducted earlier) and Ls = 2 ( from qn),
On substitution,
3 = 4 -(M*M)/2,
6 = 8-(M*M).
M*M = 2.
From the eqn of coupling coefficient,
K^2 = M^2 / (L1*L2),
K^2 = 2/ (4*2),
K^2 = 1/4,
K = 1/2 .
K= 0.5 (Answer).
(1)
Sam said:
5 years ago
1st case. Open circuit 3&4.
Kvl in loop1.
V1 = Lp di1/dt ---> eq1.
2nd case short circuit 3&4.
Kvl in loop1.
V1 = Lp' di2/dt +Mdi1/dt ---> eq2
Kvl in loop 2
Lsdi2/dt - Mdi1/dt
di2/dt = (M/Ls)di1/dt ---> eq 3
Put eq 3 in eq 2
V1 = Lp' di1/dt + M(M/Ls)di1/dt
V1 = ( Lp' + (M*M /Ls)) di1/dt ---> eq 4
Compare eq 1 and eq 4
Lp = (Lp' + (M*M /Ls)).
M^2 = 2.
K^2 = M^2 / (L1*L2),
K^2 = 2/ (4*2),
K^2 = 1/4,
K = 1/2 .
K= 0.5 (Answer).
Kvl in loop1.
V1 = Lp di1/dt ---> eq1.
2nd case short circuit 3&4.
Kvl in loop1.
V1 = Lp' di2/dt +Mdi1/dt ---> eq2
Kvl in loop 2
Lsdi2/dt - Mdi1/dt
di2/dt = (M/Ls)di1/dt ---> eq 3
Put eq 3 in eq 2
V1 = Lp' di1/dt + M(M/Ls)di1/dt
V1 = ( Lp' + (M*M /Ls)) di1/dt ---> eq 4
Compare eq 1 and eq 4
Lp = (Lp' + (M*M /Ls)).
M^2 = 2.
K^2 = M^2 / (L1*L2),
K^2 = 2/ (4*2),
K^2 = 1/4,
K = 1/2 .
K= 0.5 (Answer).
ANAMIKA said:
6 years ago
Please explain how coefficient of coupling is 0.5.
When secondary open in both coil currents are going into coil.
i.e. Lp+M = 4.
And when secondary short circuited current in primary is going into coil and current in secondary coming out of coil,
i.e.
Lp-M =3.
From above Lp=3.5 and M= 0.5.
And coefficient of coupling is -
k= M/(Lp*Ls)^1/2.
k= 0.5/(3.5*2)^1/2.
k=0.188.
When secondary open in both coil currents are going into coil.
i.e. Lp+M = 4.
And when secondary short circuited current in primary is going into coil and current in secondary coming out of coil,
i.e.
Lp-M =3.
From above Lp=3.5 and M= 0.5.
And coefficient of coupling is -
k= M/(Lp*Ls)^1/2.
k= 0.5/(3.5*2)^1/2.
k=0.188.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers