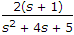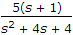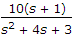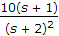Electronics and Communication Engineering - Automatic Control Systems - Discussion
Discussion Forum : Automatic Control Systems - Section 1 (Q.No. 6)
6.
In the given figure shows pole-zero plot. If steady state gain is 2 the transfer function G(s) is
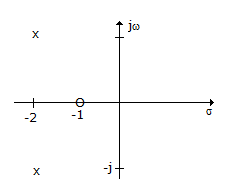
Answer: Option
Explanation:
The zero at - 1 gives the term (s + 1) in the numerator.
The poles at (- 2 + j1) and (- 2 - j1) give (s2 + 4s + 5) term is the denominator. Gain is 2.
Discussion:
9 comments Page 1 of 1.
Dadkarim said:
2 years ago
Here, we have two poles at "a = S-2+j", "b = S-2-j" and a zero at "o = S + 1".
Now let's construct the T.F equation:
G(S) = K(S+1)/(S-2+j)(S-2-j),
=K(S+1)/(S-2)^2 - j^2,
=K(S+1)/S^2+4S+5.
Also given that steady-state gain is 2. i.e.,
G(0) = 2 = K(0+1)/0^2+4(0)+5.
Solving this will give us K = 10.
Thus;
G(S) = =10(S+1)/S^2+4S+5.
Now let's construct the T.F equation:
G(S) = K(S+1)/(S-2+j)(S-2-j),
=K(S+1)/(S-2)^2 - j^2,
=K(S+1)/S^2+4S+5.
Also given that steady-state gain is 2. i.e.,
G(0) = 2 = K(0+1)/0^2+4(0)+5.
Solving this will give us K = 10.
Thus;
G(S) = =10(S+1)/S^2+4S+5.
(1)
Hijazi said:
7 years ago
The steady state is 2/5 and not 2.
(1)
Laksh said:
8 years ago
Thank you @Priti.
Priti said:
8 years ago
(-2+j)=a and (-2-j)=b.
Lets see,
How is equation made?
s^2-(a+b)s+a*b.
Lets see,
How is equation made?
s^2-(a+b)s+a*b.
(1)
Sudeep sharma said:
9 years ago
The poles at (-2+j) and (-2-j), gives the term [s-(-2+j)].[s-(-2-j)] in denominator. Solve this and get (s^2+4s+5) term in the denominator.
(1)
Shailaja said:
9 years ago
How to convert roots into an equation? Please explain.
YASH NAGARIA said:
10 years ago
@Kanna, you can consider any number as system gain.
Kanna said:
1 decade ago
Why the gain was considered as 2?
Himanshu said:
1 decade ago
How to convert roots into an equation?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers