Electronics and Communication Engineering - Automatic Control Systems - Discussion
Discussion Forum : Automatic Control Systems - Section 1 (Q.No. 8)
8.
For the system of the given figure, the damping ratio of closed loop poles is
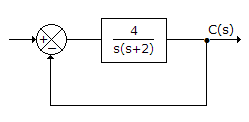
Answer: Option
Explanation:
The standard form of characteristic equation is 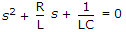 .
.
Therefore 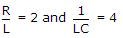 .
.
Discussion:
8 comments Page 1 of 1.
Anargul said:
7 years ago
0.25 is correct.
(2)
Sachin said:
8 years ago
4/s^2+2s ... Now divide numerator and denominator by 4, which yields 1/0.25s^2+0.5s.
Now,
2*(damping ratio)*wn = 0.5, where wn=squareroot(0.25)=0.5!
2*(damping ratio)*0.5=0.5
Damping ratio = (0.5/0.5)/2 = 0.5!
Damping ratio=0.5.
Now,
2*(damping ratio)*wn = 0.5, where wn=squareroot(0.25)=0.5!
2*(damping ratio)*0.5=0.5
Damping ratio = (0.5/0.5)/2 = 0.5!
Damping ratio=0.5.
Soundarya said:
8 years ago
How it will become 0.5 correct answer is 0.25 because;
The second order closed loop system is 4/S^2+S+4.
So
(natural frequency)^2=4 so natural freq is =2.
Then
2*damping ratio*natural frequency=1.
damping ratio=0.25.
The second order closed loop system is 4/S^2+S+4.
So
(natural frequency)^2=4 so natural freq is =2.
Then
2*damping ratio*natural frequency=1.
damping ratio=0.25.
Abhishek Singh Agnivanshi said:
9 years ago
The correct answer is 0.25 only because it is asking for closed loop damping ratio and not open pole.
Shivani said:
9 years ago
Thanks @Soumya.
SHREYAS said:
10 years ago
Thank you so much @Soumya.
Soumya Ranjan Patra said:
1 decade ago
We know, Time response of 2nd order system:
G(s)= (natural freq.)^2/ s(s+2*damping ratio*natural freq.).
Comparing with question, G(s)=4/s(s+2).
So,
(natural freq.)^2=4 =>natural freq. = 2 &
2*damping ratio*natural freq. = 2.
=> 2*damping ratio*2 = 2.
=>damping ratio = 0.5.
G(s)= (natural freq.)^2/ s(s+2*damping ratio*natural freq.).
Comparing with question, G(s)=4/s(s+2).
So,
(natural freq.)^2=4 =>natural freq. = 2 &
2*damping ratio*natural freq. = 2.
=> 2*damping ratio*2 = 2.
=>damping ratio = 0.5.
Lalitha said:
1 decade ago
Also can be found as:
From the closed loop transfer function,
Natural frequency = 2 rad/s.
2*damping ratio*natural frequency = 2.
Implies 2*damping ratio*2 = 2.
Implies damping ratio=1/2 = 0.5.
From the closed loop transfer function,
Natural frequency = 2 rad/s.
2*damping ratio*natural frequency = 2.
Implies 2*damping ratio*2 = 2.
Implies damping ratio=1/2 = 0.5.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers