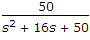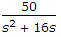IndiaBIX

Electronics and Communication Engineering - Automatic Control Systems

Exercise : Automatic Control Systems - Section 1
36.
In Bode diagram (log magnitude plot) the factor in the transfer function gives a line having slope
-20 dB per octave
-10 dB per octave
-6 dB per octave
-2 dB per octave
Answer: Option
Explanation:

For term the slope is -20 dB/decade or -6 dB/octave because - 20 log 2 = -6 dB.

37.
In the given figure the input is x(t) = A sin ωt. The steady state output y(t) =
A sin (ωt + φ) where φ = tan-1 |G(jω)|
|G(jω)| A sin [ωt + ∠G(jω)]
|G(jω)| A sin [2ωt + ∠G(jω)]
A G(jω) sin [ωt + ∠G(jω)]
Answer: Option
Explanation:

The magnitudes A and G(jω) are multiplied and phase angles are added.

38.
In the given figure x6 =
de(ax1 + bx2 + cx3)
(a + b + c) (x1 + x2 + x3) (d + e)
(ax1 + bx2 + cx3) (d + e)
a b c d e (x1 + x2 + x3)
Answer: Option
Explanation:

The input x1 is multiplied by a, x2, by b and x3 by c. The sum total is multiplied by d and e.

39.
A negative feedback system has . The closed loop system is stable for
K > 20
15 < K < 19
8 ≤ K ≤ 14
K < 6
Answer: Option
Explanation:

Find characteristic equation.

40.
For the given figure,
Answer: Option
Explanation:

For the inner loop, transfer function =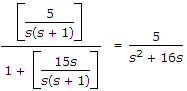

Then .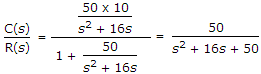

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers