Electrical Engineering - Circuit Theorems and Conversions - Discussion
Discussion Forum : Circuit Theorems and Conversions - General Questions (Q.No. 5)
5.
Find the current through R2 of the given circuit.
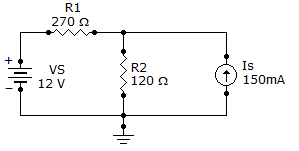

Discussion:
21 comments Page 1 of 3.
Dhanaraj K said:
4 years ago
Apply current division method.
I at (R2)= r1 *I/r1 + r2.
I at (R2)= r1 *I/r1 + r2.
(3)
Anon said:
6 years ago
By nodal analysis we will arrived to this equation;
(V-12)/270 + V/120 -150mA =0 .
V=16.15V.
Hence,
I2=16.15/120.
I2=1.346mA.
(V-12)/270 + V/120 -150mA =0 .
V=16.15V.
Hence,
I2=16.15/120.
I2=1.346mA.
(8)
Fayaz said:
8 years ago
16.15/120=.134amp.
134/1000=1.34ma.
134/1000=1.34ma.
(3)
Md, Rayhan Uddin said:
8 years ago
0 = V-12/270 + V/120 " 0.15,
=>(4V-48+9V-162)=0,
=>13V=210,
=>V=210/13,
=>V=16.15V,
Since, IR2=16.15/120,
=134mA.
=>(4V-48+9V-162)=0,
=>13V=210,
=>V=210/13,
=>V=16.15V,
Since, IR2=16.15/120,
=134mA.
D.MAHAMMAD ALI said:
9 years ago
By nodal annalysis first find node voltage then find the current.
(1)
Basireddy said:
9 years ago
Write loop equation.
270(i1)+120(i1+i2)=12V ..........eqn-1
And i2=150mA.
Now solving eqn-1.
270(i1)+120(i1)+(120*150mA) = 12V
390(i1)+18V = 12V
390(i1) =12V-18V
390(i1) = -6V
i1 = -6V/390
i1 = -15.38mA
Now current flowing through R2 is (i1 + i2).
Therefore, -15.38mA + 150mA = 134.62mA.
270(i1)+120(i1+i2)=12V ..........eqn-1
And i2=150mA.
Now solving eqn-1.
270(i1)+120(i1)+(120*150mA) = 12V
390(i1)+18V = 12V
390(i1) =12V-18V
390(i1) = -6V
i1 = -6V/390
i1 = -15.38mA
Now current flowing through R2 is (i1 + i2).
Therefore, -15.38mA + 150mA = 134.62mA.
(5)
Jagadesh said:
10 years ago
By applying nodal analysis.
Current entering = Current leaving.
Assume the 120 ohm branch node as v.
150 mA = ((V - 12)/270) + (V/120).
0.15 = (13 V - 48)/1080.
162 = 13V - 48.
13 V = 210.
V = 210/13 V.
Current in 120 ohm branch = V/120.
= 210/(13*120).
= 7/(13*4) = 7/52 = 0.134.
= 134 mA.
Current entering = Current leaving.
Assume the 120 ohm branch node as v.
150 mA = ((V - 12)/270) + (V/120).
0.15 = (13 V - 48)/1080.
162 = 13V - 48.
13 V = 210.
V = 210/13 V.
Current in 120 ohm branch = V/120.
= 210/(13*120).
= 7/(13*4) = 7/52 = 0.134.
= 134 mA.
(1)
Vignesh said:
1 decade ago
Please tell this problem.
Dusmanta rohiodas said:
1 decade ago
0 = V-12/270 + V/120 + 150.
V = 16.15.
Current through R2.
I = V/R.
= 16.15/120.
= 134 mA.
V = 16.15.
Current through R2.
I = V/R.
= 16.15/120.
= 134 mA.
(4)
Amke naveen said:
1 decade ago
Use super position theorem first consider dc voltage source open current source.
So i1 = 12/270+120.
Then current source i2 = 150m*270/270+120.
I = i1+i2.
So i1 = 12/270+120.
Then current source i2 = 150m*270/270+120.
I = i1+i2.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers