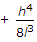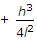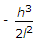Civil Engineering - UPSC Civil Service Exam Questions - Discussion
Discussion Forum : UPSC Civil Service Exam Questions - Section 14 (Q.No. 41)
41.
During the measurement of a line by chain or tape in slopes, if the length of the line is 'l' and the height difference between the ends of the line is 'h', then the correction to the measured length is more than 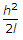 by
by
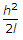 by
byDiscussion:
3 comments Page 1 of 1.
Krish Pandit said:
5 years ago
Correction due to slope.
Cs = True value - measured value.
= root(L^2 - H^2) - L.
= L x [1- (H^2 / L^2)]^0.5 - L = { L [ 1- 0.5*(H^2 / L^2) + [0.5*(0.5-1)*(H^2 / L^2)^2 / 2] } - L.
= L - L* 0.5*(H^2 / L^2) + L* [0.5*(0.5-1)*(H^2 / L^2)^2 / 2 - L.
= -(H^2)/2L - (H^4)/8*L^3.
So, the correction to the measured length is more than by (H^4)/8*L^3*.
Cs = True value - measured value.
= root(L^2 - H^2) - L.
= L x [1- (H^2 / L^2)]^0.5 - L = { L [ 1- 0.5*(H^2 / L^2) + [0.5*(0.5-1)*(H^2 / L^2)^2 / 2] } - L.
= L - L* 0.5*(H^2 / L^2) + L* [0.5*(0.5-1)*(H^2 / L^2)^2 / 2 - L.
= -(H^2)/2L - (H^4)/8*L^3.
So, the correction to the measured length is more than by (H^4)/8*L^3*.
(3)
Sangeetha said:
6 years ago
Cslope = Actual length - Measured length.
= sqrt(L^2 - H^2) - L.
= L x [1- (H^2 / L^2)]^0.5 - L = { L [ 1- 0.5*(H^2 / L^2) + [0.5*(0.5-1)*(H^2 / L^2)^2 / 2] } - L.
= L - L* 0.5*(H^2 / L^2) + L* [0.5*(0.5-1)*(H^2 / L^2)^2 / 2 - L.
= -(H^2)/2L - (H^4)/8*L^3.
Hence, correction to the measured length is more than by (H^4)/8*L^3.
= sqrt(L^2 - H^2) - L.
= L x [1- (H^2 / L^2)]^0.5 - L = { L [ 1- 0.5*(H^2 / L^2) + [0.5*(0.5-1)*(H^2 / L^2)^2 / 2] } - L.
= L - L* 0.5*(H^2 / L^2) + L* [0.5*(0.5-1)*(H^2 / L^2)^2 / 2 - L.
= -(H^2)/2L - (H^4)/8*L^3.
Hence, correction to the measured length is more than by (H^4)/8*L^3.
(3)
Drone said:
8 years ago
How? someone explain.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers