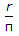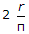Civil Engineering - Theory of Structures - Discussion
Discussion Forum : Theory of Structures - Section 3 (Q.No. 14)
14.
Shear centre of a half circular section of radius r and of constant thickness, lies at a distance of x from the centre where x is
Discussion:
4 comments Page 1 of 1.
Piyush said:
3 years ago
Shear centre = b^2 h^2 t/4I.
Here,
b = d,
h = d/2.
I= π/4 d^4.
Shear centre=d^2 . (d/2)^2 . d/4 . (π/4 d^4)
= 8D/&pi.
= 4r/π.
Here,
b = d,
h = d/2.
I= π/4 d^4.
Shear centre=d^2 . (d/2)^2 . d/4 . (π/4 d^4)
= 8D/&pi.
= 4r/π.
Shubham said:
5 years ago
@Mustafa Kamal.
How t = d/4?
How t = d/4?
Mustafa kamal said:
6 years ago
shear centre=b^2 h^2 t/4I.
Here,
b=d,
h=d/2.
I=pi/4 d^4
Shear centre=d^2 . (d/2)^2 . d/4 . (pi/4 d^4)
=8D/pi.
=4r/pi.
Here,
b=d,
h=d/2.
I=pi/4 d^4
Shear centre=d^2 . (d/2)^2 . d/4 . (pi/4 d^4)
=8D/pi.
=4r/pi.
Skm said:
8 years ago
Can Anyone explain it?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers