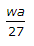Civil Engineering - Theory of Structures - Discussion
Discussion Forum : Theory of Structures - Section 1 (Q.No. 19)
19.
A simply supported beam carries varying load from zero at one end and w at the other end. If the length of the beam is a, the maximum bending moment will be
Discussion:
8 comments Page 1 of 1.
Vaibhav Tatawar said:
5 years ago
Thanks for explaining @Llokesh Sahu.
Sandeep kshetri said:
7 years ago
How the reaction at support b is negative? it would be positive.
Ankit said:
7 years ago
Well said, Thanks, @Lokesh.
Nami said:
8 years ago
Thanks @Lokesh.
Really good explanation.
Really good explanation.
Lokesh Sahu said:
8 years ago
Let reaction loads are RA & RB @ point A & B.
RA+RB=wl/2.
To calculating we found RA= wl/6 & RB= -wl/3,
let take a section X-X @ a distance of x from A.
UVL will be @ X-X = wx/l,
& load on triangle ACX = wx2 /2l,
& find the SF @ X-X,
Fx= RA - load on triangle ACX,
Fx=( wl/6) - (wx2/2l) -------> (1)
Fx at A will be. X=0
Fx = wl/6
Fx at B will be. X=l
Fx=-wl/3.
Moment will be max, where Fx=0,
So, x= l/(3)1/2.
Now find the moment at X-X.
Mx = (RA*x) " (load on triangle ACX * x/3)load of the triangle will be act ta 1/3rd distance from A.
Mx= (wlx/6) " (wx3/6l)
Moment at x= l/(3)1/2
Mx= (wl*( l/(3)1/2)/6) - (w*( l/(3)1/2)3/6l)
Mx= wl2/9(3)1/2.
RA+RB=wl/2.
To calculating we found RA= wl/6 & RB= -wl/3,
let take a section X-X @ a distance of x from A.
UVL will be @ X-X = wx/l,
& load on triangle ACX = wx2 /2l,
& find the SF @ X-X,
Fx= RA - load on triangle ACX,
Fx=( wl/6) - (wx2/2l) -------> (1)
Fx at A will be. X=0
Fx = wl/6
Fx at B will be. X=l
Fx=-wl/3.
Moment will be max, where Fx=0,
So, x= l/(3)1/2.
Now find the moment at X-X.
Mx = (RA*x) " (load on triangle ACX * x/3)load of the triangle will be act ta 1/3rd distance from A.
Mx= (wlx/6) " (wx3/6l)
Moment at x= l/(3)1/2
Mx= (wl*( l/(3)1/2)/6) - (w*( l/(3)1/2)3/6l)
Mx= wl2/9(3)1/2.
(2)
Muzzamil said:
8 years ago
It is 2wl/9*√ 3.
Prem khandeep said:
9 years ago
According to me, It is wl^2÷9 √3EI.
Ferd said:
10 years ago
It should be :(2wa^2)/(9 * square root of 3).
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers