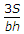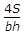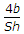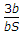Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 22)
22.
A triangular section having base b, height h, is placed with its base horizontal. If the shear stress at a depth y from top is q, the maximum shear stress is
Discussion:
21 comments Page 1 of 3.
Prem prakash said:
5 years ago
What is the use of q? Please explain.
Harsh Sharma said:
6 years ago
Qmax= (3/2)* Qavg -----------> (i)
Qavg = S/A.
Where S= Shear Force.
And A= (b*h)/2.
Hence, Qavg= 2S/(b*h) ----------> (ii)
Now from (i) & (ii).
Qmax = (3/2)* {2S/(b*h)}.
i.e. Qmax = 3S/(b*h).
Qavg = S/A.
Where S= Shear Force.
And A= (b*h)/2.
Hence, Qavg= 2S/(b*h) ----------> (ii)
Now from (i) & (ii).
Qmax = (3/2)* {2S/(b*h)}.
i.e. Qmax = 3S/(b*h).
(9)
Sachin s naik said:
7 years ago
Thank you @Krishna.
PRASENJIT said:
7 years ago
For triangular section:
Qmax = Qav*h^2/(12*I) ---> Eqn 1.
Again I for triangular section= 1/36 bh^3.
Now you put the value of "I" in equation no.1.
You will get the answer as option A.
Here Qav is denoted by S.
Qmax = Qav*h^2/(12*I) ---> Eqn 1.
Again I for triangular section= 1/36 bh^3.
Now you put the value of "I" in equation no.1.
You will get the answer as option A.
Here Qav is denoted by S.
Amu bokato said:
7 years ago
Thank you @Krishna.
Sakib said:
7 years ago
Why 1.5? It should be multiflied by 4/3.
(2)
Khemraj bind said:
7 years ago
S = shear stress.
Area of triangle=0.5 * bh.
Maximum shear stress of triangle = Average shear stress of triangle 3/2.
= (3/2) * S/A,
= (1.5 S) /0.5 bh,
= 3S/bh.
The correct answer is option A.
Area of triangle=0.5 * bh.
Maximum shear stress of triangle = Average shear stress of triangle 3/2.
= (3/2) * S/A,
= (1.5 S) /0.5 bh,
= 3S/bh.
The correct answer is option A.
Krutarth said:
7 years ago
Why 1.5* S?
Ziya said:
8 years ago
S = Shear force.
Maximum shear stress = 3S/bh.
Maximum shear stress = 3S/bh.
Sheela said:
8 years ago
Thanks @Krishna.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers