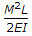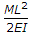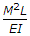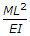Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 49)
49.
The energy stored in a beam of length L subjected to a constant B.M. is
Discussion:
11 comments Page 1 of 2.
Sanchet said:
4 years ago
U=(integration of (M^2dx))1/2EI from 0 to L.
= (M^2x)/2EI 0 to L.
= M^2L/2EI.
= (M^2x)/2EI 0 to L.
= M^2L/2EI.
(3)
Pakistan said:
5 years ago
Strain Energy=1/2 * Moment * slope.
Slope= ML/EI.
Moment = M.
Strain Energy = 1/2 * M * ML/EI.
= (1/2 M^2 L/EI).
Slope= ML/EI.
Moment = M.
Strain Energy = 1/2 * M * ML/EI.
= (1/2 M^2 L/EI).
(8)
Rajbir said:
6 years ago
I think B is the correct answer.
Vipin sainath said:
6 years ago
Slopes may differ according to support conditions.
How did you take ML/EI? @Jeevan.
How did you take ML/EI? @Jeevan.
Sumant said:
7 years ago
Thank you @Jeevan.
Jeevan said:
7 years ago
Strain Energy=1/2 * Moment * slope.
Slope= ML/EI.
Moment=M.
Strain Energy = 1/2*M*ML/EI.
= (1/2 M^2 L/EI).
Slope= ML/EI.
Moment=M.
Strain Energy = 1/2*M*ML/EI.
= (1/2 M^2 L/EI).
(2)
Dhanu said:
8 years ago
It's an derivation for strain energy due to bending.
Dax said:
9 years ago
Maybe you should find the answer in strain energy stored in linear elastic system theory.
Guduli said:
10 years ago
Can anyone explain this?
S.PRAVINKUMAR said:
10 years ago
How to calculate the derivation?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers