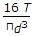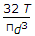Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 5 (Q.No. 22)
22.
A solid circular shaft of diameter d is subjected to a torque T. The maximum normal stress induced in the shaft, is
Discussion:
21 comments Page 1 of 3.
Mian Khan said:
1 year ago
I think Option A is correct.
When a solid circular shaft is subjected to a torque (T), the maximum stress induced in the shaft is shear, not normal stress. The maximum normal stress is theoretically zero in pure torsion.
When a solid circular shaft is subjected to a torque (T), the maximum stress induced in the shaft is shear, not normal stress. The maximum normal stress is theoretically zero in pure torsion.
Pankaj Pokhrel said:
3 years ago
For pure torsion in a shaft, normal stress is zero. So, A should be the right answer.
Dipunku said:
6 years ago
It should be the shear stress.
(1)
Naveen said:
6 years ago
Torque equation T/J =F/R.
F=TR/J.
We know R=d/2.
Polar modulus J=pi d^4/32.
Then substitute we can get the given answer.
F=TR/J.
We know R=d/2.
Polar modulus J=pi d^4/32.
Then substitute we can get the given answer.
Kvk said:
6 years ago
In the case of pure torsion, the beam element is under pure shear.
In pure shear case, the principal stresses are equal to shear stress acting on the element.
So, here maximum normal shear stress is equal to maximum shear stress.
In pure shear case, the principal stresses are equal to shear stress acting on the element.
So, here maximum normal shear stress is equal to maximum shear stress.
(1)
Bipin Dhungana said:
6 years ago
As per torsional formula :
T = Stress*polar modulus.
Stress = T/Z.
Z = pi*d3/16.
Stress = 16T/pi*d3.
T = Stress*polar modulus.
Stress = T/Z.
Z = pi*d3/16.
Stress = 16T/pi*d3.
(1)
Nirz said:
7 years ago
[T/{j=(Ix+Iy)}]=(Ï„/R),
> (T*R)÷j = τ.
>(T*2D)÷(π*D^4/32) = Ï„.
>(T*16)/π*D^3 = Ï„.
> (T*R)÷j = τ.
>(T*2D)÷(π*D^4/32) = Ï„.
>(T*16)/π*D^3 = Ï„.
Shubham Rawat said:
7 years ago
Answer B.
It is based on pure shear case σ = τ.
It is based on pure shear case σ = τ.
Utsav said:
7 years ago
A is correct.
B is for max shear stress.
C is for max bending stress.
B is for max shear stress.
C is for max bending stress.
Siddhant said:
8 years ago
The max normal stress for a combination of b.m and torsion is given by;
16(M+(M(sq)+T(sq))^.5/(π)D^3.
put M = 0 in this equation.
16(M+(M(sq)+T(sq))^.5/(π)D^3.
put M = 0 in this equation.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers