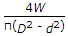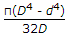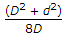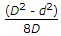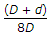Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 2 (Q.No. 43)
43.
The greatest eccentricity which a load W can have without producing tension on the cross-section of a short column of external diameter D and internal diameter d, is
Discussion:
5 comments Page 1 of 1.
Jaz said:
6 years ago
I= π/64(D^4 - d^'4).
Area = π/4(D^2 - d^2).
I = AK^2.
K^2 = I/A.
=π/64{D^4-d^4}/π/4{D^2-d^2}
= D^2 + d^2/16.
e= 2K^2/D.
e= D^2 + d^2/8D.
Area = π/4(D^2 - d^2).
I = AK^2.
K^2 = I/A.
=π/64{D^4-d^4}/π/4{D^2-d^2}
= D^2 + d^2/16.
e= 2K^2/D.
e= D^2 + d^2/8D.
Somesh said:
7 years ago
Why not option D?
Abhik said:
7 years ago
@Basha.
How e=z/a? Please explain.
How e=z/a? Please explain.
Sheela KR said:
8 years ago
Thanks @Basha.
Basha said:
8 years ago
We know that e=z/a.
now z=i/y,
i=pi*(D^4-d^4)/64
y=d/2
a=pi*(D^2-d^2)/4.
Now substitute the above values in e=z/a.
now z=i/y,
i=pi*(D^4-d^4)/64
y=d/2
a=pi*(D^2-d^2)/4.
Now substitute the above values in e=z/a.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers