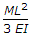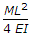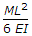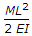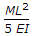Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 3 (Q.No. 47)
47.
Maximum deflection of a cantilever due to pure bending moment M at its free end, is
Discussion:
11 comments Page 1 of 2.
Asay said:
8 years ago
I think it should be Option (A) ML^2/3EI.
As we know that,
Deflection in a Cantilever due to Load P at its free end is,
PL^3/3EI
Since, M=P.L
So,
(P.L)L^2/3EI
(M)L^2/3EI
So,
Deflection=ML^2/3EI (Option A).
As we know that,
Deflection in a Cantilever due to Load P at its free end is,
PL^3/3EI
Since, M=P.L
So,
(P.L)L^2/3EI
(M)L^2/3EI
So,
Deflection=ML^2/3EI (Option A).
Ruchir Singh said:
8 years ago
Given answer is correct.
This is the standard value result.
Value of slope = ML/EI.
Value of Deflection= ML^2/2EI.
This is the standard value result.
Value of slope = ML/EI.
Value of Deflection= ML^2/2EI.
Bhaskar said:
5 years ago
Deflection = ML^2/3EL.
Max Deflection = 1.5 deflection.
=1.5 * ML^2/3EI,
=ML^2/2EI.
Max Deflection = 1.5 deflection.
=1.5 * ML^2/3EI,
=ML^2/2EI.
Gun shot said:
5 years ago
It should be wl^2/3EI for DEFLECTION.
Where as Wl^2/2EI for the SLOPE.
Where as Wl^2/2EI for the SLOPE.
Priyanka said:
7 years ago
BMD is rectangular due to this deflection is,
ML^2/EI(1/2)= ML^2/2EI.
ML^2/EI(1/2)= ML^2/2EI.
Ankit said:
8 years ago
Go through double integration method you would get the answer.
Sheela said:
8 years ago
Can't understand. Please explain in detail.
Anand kumar gupta said:
9 years ago
Please suggest me the solution.
BHUSHAN said:
10 years ago
Explain the solution part.
Kirana said:
7 years ago
Yes it should be ML^2/3EI.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers