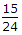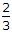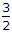Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 19)
19.
The ratio of the maximum deflections of a beam simply supported at its ends with an isolated central load and that of with a uniformly distributed load over its entire length, is
Discussion:
24 comments Page 3 of 3.
Mayuri said:
1 decade ago
Ratio is 8/5, hence multiplying by 3 we will get 24/15 which is given in options.
Bhakti deshmukh said:
1 decade ago
@Bhakti deshmukh:
1) Max. Deflection of ssb subjected to central load = WL^3/48 EI.
2) Max. Deflection of beam subjected to udl = (5wL^4)/(384EI).
Hence ratio of these two is 8/5.
1) Max. Deflection of ssb subjected to central load = WL^3/48 EI.
2) Max. Deflection of beam subjected to udl = (5wL^4)/(384EI).
Hence ratio of these two is 8/5.
Souryadeep Chaki said:
1 decade ago
Maximum deflections of a beam simply supported at its ends with an isolated central load = (WL^3)/(48EI).
Maximum deflections of a beam simply supported at its ends with uniformly distributed load= (5wL^4)/(384EI) {W=wL}.
So [(WL^3)/(48EI)] / [(5wL^4)/(384EI)] = 8/5.
Maximum deflections of a beam simply supported at its ends with uniformly distributed load= (5wL^4)/(384EI) {W=wL}.
So [(WL^3)/(48EI)] / [(5wL^4)/(384EI)] = 8/5.
MAYANK JAIN said:
1 decade ago
Maximum deflections of a beam simply supported at its ends with an isolated central load = (WL^3)/(48EI)
Maximum deflections of a beam simply supported at its ends with uniformly distributed load= (5wL^4)/(384EI) {W=wL}
So [(WL^3)/(48EI)] / [(5wL^4)/(384EI)] = 24/15.
Maximum deflections of a beam simply supported at its ends with uniformly distributed load= (5wL^4)/(384EI) {W=wL}
So [(WL^3)/(48EI)] / [(5wL^4)/(384EI)] = 24/15.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers