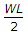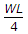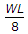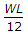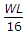Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 18)
18.
A simply supported beam of span L carries a concentrated load W at its mid-span. The maximum bending moment M is
Discussion:
5 comments Page 1 of 1.
Inayat Ullah Kakar said:
1 year ago
For a simply supported beam:
BM = Wl/4 for point load at centre.
BM = Wl^2/8 for UDL.
BM = Wl^2/12 for UVL.
BM = Wl/4 for point load at centre.
BM = Wl^2/8 for UDL.
BM = Wl^2/12 for UVL.
Shasha said:
8 years ago
What is the bending moment value for fixed support beam of span L carries the concentrated load at mid span?
Asay said:
8 years ago
Since in simply supported beams, the bending moment is zero at the support ends, So it should be maximum at the centre (i-e at point of loading).
But,
Reactions at the supports will be W/2 each.
So, Bending Moment (max) at the centre = (W/2)(L/2)=WL/4 (Option B).
But,
Reactions at the supports will be W/2 each.
So, Bending Moment (max) at the centre = (W/2)(L/2)=WL/4 (Option B).
(6)
DEVENDRANAIK said:
9 years ago
IN SIMPLE SUPPORTED BEAM of length L.
Then the reactions at each ends = W/2.
Then we calculate the half if the length of the beam = L/2 (L=length of the beam is L).
HERE SHEAR FORCE = WL/2 (from the left end).
BENDING MOMENT = W/2 * L/2 = WL/4.
Then the reactions at each ends = W/2.
Then we calculate the half if the length of the beam = L/2 (L=length of the beam is L).
HERE SHEAR FORCE = WL/2 (from the left end).
BENDING MOMENT = W/2 * L/2 = WL/4.
(2)
Vinay said:
1 decade ago
Support reactions = w/2,
Max bending moment occurs at point of loading acting for symmetrical loading,
= w/2*l/2
= wl/4
Max bending moment occurs at point of loading acting for symmetrical loading,
= w/2*l/2
= wl/4
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers