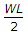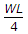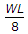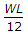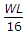Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 2 (Q.No. 11)
11.
A simply supported beam of span L carries a uniformly distributed load W. The maximum bending moment M is
Discussion:
19 comments Page 2 of 2.
Kallan said:
8 years ago
wl = W thats why WL/8.
Deepak Singh Bisht said:
8 years ago
Wl^2/8 is the right answer.
Mohit Swaraj said:
9 years ago
It should be (wl^2)÷8.
Prasad pawar said:
9 years ago
It is WL^2/8.
Baloch said:
9 years ago
I agree that the correct answer is wl^2 / 8.
Sachin said:
9 years ago
According to me, the correct answer is WL^2/8 not wl/8.
P.kishore said:
9 years ago
S L be the length of span kn/m total udl then we calculate maximum bending moment = force * distance.
And also half of the total udl distance then wl^2/8.
And also half of the total udl distance then wl^2/8.
VINAYAK said:
1 decade ago
Due to symmetric loading, reactions are equal having magnitude = WL/2.
The maximum moment will occurs at center of span because of symmetric loading.
Take moment at this point,
Maximum bending moment = (WL/2) (L/2) - (WL/2) (L/4) = WL^2/8.
The maximum moment will occurs at center of span because of symmetric loading.
Take moment at this point,
Maximum bending moment = (WL/2) (L/2) - (WL/2) (L/4) = WL^2/8.
Mounika reddy said:
1 decade ago
Support reactions are Vay = wl/2 = Vby.
Cut s/n and take the moment at pont zero.
M = - (wx^2/2) +wlx/2.
Max moment at mid pnt l/2.
M = Wl^2/8.
For uniformly distributed load moment varies parabolically not linearly.
Cut s/n and take the moment at pont zero.
M = - (wx^2/2) +wlx/2.
Max moment at mid pnt l/2.
M = Wl^2/8.
For uniformly distributed load moment varies parabolically not linearly.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers