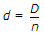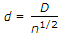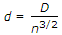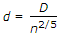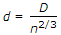Civil Engineering - Hydraulics - Discussion
Discussion Forum : Hydraulics - Section 4 (Q.No. 16)
16.
To replace a pipe of diameter D by n parallel pipes of diameter d, the formula is
Discussion:
5 comments Page 1 of 1.
Shubham yadav said:
5 years ago
Here discharge through Pipe of dia 'D'= Q.
Discharge through one pipe of dia 'd'= q.
So, Total discharge through 'n' no. Of pipes od dia 'd' = n*q
Now if we replace the big dia pipe by small dia pipe then discharge has to be same
Q=nq.
Squaring both sides
Q^2=n^2.q^2 ----------> (1)
Put the value of Q^2 and q^2 by using formulae.
H=(flQ^2)/(12*D^5)
Value of f, l and h will be same for both pipes for the same discharge.
So, eqn 1 becomes;
D^5 = n^2*d^5.
d = D/n^(2/5).
Discharge through one pipe of dia 'd'= q.
So, Total discharge through 'n' no. Of pipes od dia 'd' = n*q
Now if we replace the big dia pipe by small dia pipe then discharge has to be same
Q=nq.
Squaring both sides
Q^2=n^2.q^2 ----------> (1)
Put the value of Q^2 and q^2 by using formulae.
H=(flQ^2)/(12*D^5)
Value of f, l and h will be same for both pipes for the same discharge.
So, eqn 1 becomes;
D^5 = n^2*d^5.
d = D/n^(2/5).
Riju Das said:
5 years ago
Here , h and l will be same.
flQ^2/12.1D^2= (n) flQ^2/12.1d^2.
So, d=D/n^(2/5).
flQ^2/12.1D^2= (n) flQ^2/12.1d^2.
So, d=D/n^(2/5).
Vishal Sharma said:
7 years ago
If Length is constant then,
D^2/5 = nd^2/5,
d = D/n^5/2.
D^2/5 = nd^2/5,
d = D/n^5/2.
Pogisidave said:
7 years ago
Please, Can you elaborate the formula?
Mahesh sinh said:
9 years ago
We derive it n = (D/d)^5/2.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers