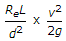Civil Engineering - Hydraulics - Discussion
Discussion Forum : Hydraulics - Section 1 (Q.No. 40)
40.
In a circular pipe of length L and diameter d, a viscous liquid is flowing with a velocity v. The loss in head, is
Discussion:
8 comments Page 1 of 1.
Hemanth said:
3 years ago
hf = FLV^2/2gd.
Coefficient of friction f = 16/Re,
F=4f=4*16/Re.
Substitute all in the formula of hf.
So, A is the correct answer.
Coefficient of friction f = 16/Re,
F=4f=4*16/Re.
Substitute all in the formula of hf.
So, A is the correct answer.
(2)
Harsha said:
9 years ago
Friction factor f = 64/re re-reynolds no.
Man singh said:
8 years ago
Friction factor for reynold no f = 16/re.
Anomi said:
8 years ago
hf=f.l.v^2/2gd,
f=64/Re.
f=64/Re.
Naveen Venkat said:
8 years ago
F = 64/Re - friction factor.
Co-efficient of friction f = 16/Re,
Therefore F = 4f =4 * 16/Re.
Co-efficient of friction f = 16/Re,
Therefore F = 4f =4 * 16/Re.
Nilraj said:
7 years ago
Thanks @Naveen.
Bk prajapati said:
4 years ago
I think B is the right answer.
Priyan said:
9 months ago
The correct answer to the question can be determined using the Darcy-Weisbach equation for head loss in a pipe:
hf = frac{4 f L v^2}{2 g d}.
For laminar flow, the Darcy friction factor () is given by:
f = frac{16}{Re}.
where Reynolds number () is:
Re = frac{ρ v d}{mu}.
Substituting into the equation:
hf = frac{16}{Re} times frac{4L}{d} times frac{v^2}{2g}.
hf = frac{16}{Re} times frac{4L}{d} times frac{v^2}{2g}.
Comparing this with the given options, option (A) is the correct answer:
frac{16}{Re}times frac{4L}{d} times frac{v^2}{2g}.
hf = frac{4 f L v^2}{2 g d}.
For laminar flow, the Darcy friction factor () is given by:
f = frac{16}{Re}.
where Reynolds number () is:
Re = frac{ρ v d}{mu}.
Substituting into the equation:
hf = frac{16}{Re} times frac{4L}{d} times frac{v^2}{2g}.
hf = frac{16}{Re} times frac{4L}{d} times frac{v^2}{2g}.
Comparing this with the given options, option (A) is the correct answer:
frac{16}{Re}times frac{4L}{d} times frac{v^2}{2g}.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers