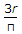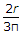Civil Engineering - Applied Mechanics - Discussion
Discussion Forum : Applied Mechanics - Section 2 (Q.No. 14)
14.
The distance of the c.g. of a semi-circular arc of radius r from its diameter along the radius of symmetry, is
Discussion:
11 comments Page 1 of 2.
Agha Bilal said:
1 year ago
The distance of the centre of gravity (c.g) of a semi-circular arc of radius (r) from its diameter along the radius of symmetry is given by: 2r/π.
This formula provides the perpendicular distance from the diameter (the straight edge of the semi-circular arc) to the c.g. along the radius of symmetry.
This formula provides the perpendicular distance from the diameter (the straight edge of the semi-circular arc) to the c.g. along the radius of symmetry.
Krishna Yadav said:
2 years ago
Both semicircle (4r/3π) and semicircular arc (2r/π) are 2D the difference is that arc is basically a hollow semicircle it is like a wire making half perimeter of the circle only.
(2)
Suresh Thakur said:
5 years ago
4r/3π is correct because CG of the semi-circular arc is asked not semi-circular area.
Pavi said:
7 years ago
@Jay.
How do you know it's 2D semi-circular?
I think 4r/3π is correct.
How do you know it's 2D semi-circular?
I think 4r/3π is correct.
(1)
Jay solanki said:
7 years ago
The correct answer is 2r/π.
It is a 2D semicircular arc.
It is a 2D semicircular arc.
Shubham Gadge said:
5 years ago
CG of semi-circular arc is 2r/π.
(1)
Shivam said:
7 years ago
Can anybody please explain this?
Subha Annadurai said:
8 years ago
C.G of semicircle = 4r/3π.
Anish Bera said:
6 years ago
4r/3π is the correct one.
Xiyaz said:
9 years ago
2r/π is the correct one.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers