Chemical Engineering - Fluid Mechanics - Discussion
Discussion Forum : Fluid Mechanics - Section 4 (Q.No. 41)
41.
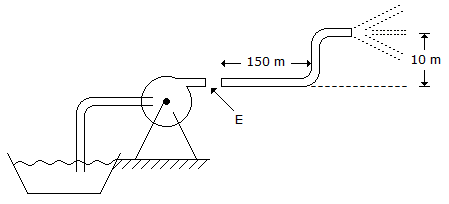
A centrifugal pump is used to pump water through a horizontal distance of 150 m, and then raised to an overhead tank 10 m above. The pipe is smooth with an I.D of 50 mm. What head (m of water) must the pump generate at its exit (E) to deliver water at a flow rate of 0.001 m3/s? The Fanning friction factor, f is 0.0062.

Discussion:
4 comments Page 1 of 1.
AMAL ABRAHAM said:
3 years ago
hm = 10 + hf (BERNOULLI'S EQUATION) ---------> (1)
hf = 4flv^2/2gD (DARCY'S EQUATION) -----------> (2)
v = Q/A ----------------------------- > (3)
Put (3) in (2) hf = 0.98 ---------------> (4)
Put (4) in (1).
hm = 10 + 0.98 = 10.98.
Hence,
Option B - 11 m.
hf = 4flv^2/2gD (DARCY'S EQUATION) -----------> (2)
v = Q/A ----------------------------- > (3)
Put (3) in (2) hf = 0.98 ---------------> (4)
Put (4) in (1).
hm = 10 + 0.98 = 10.98.
Hence,
Option B - 11 m.
(3)
Addisu erku said:
4 years ago
It is a good calculation, but I want to know the parallel pump system discharge head and pipe diameter analysis formula because it has the same Q1 and Q2, if it Is Not Equal the Sum Of The Two in The Case Of Pressure.
Jomson Mathachan said:
7 years ago
Total Length of pipe = 150m + 10m = 160m.
D = 0.05m,
Q = 0.001 m^3 /s,
Q = A*V,
0.001 = (3.14/4)* 0.05^2 * V.
V = 0.509 m/s.
Head Loss = (4 * f * L * v^2)/(2 * g * D).
= 1.05m.
Velocity head = v^2/ 2g.
= 0.013m.
Total Head (m of water) = 1.05 + 0.013 + 10 = 11m.
D = 0.05m,
Q = 0.001 m^3 /s,
Q = A*V,
0.001 = (3.14/4)* 0.05^2 * V.
V = 0.509 m/s.
Head Loss = (4 * f * L * v^2)/(2 * g * D).
= 1.05m.
Velocity head = v^2/ 2g.
= 0.013m.
Total Head (m of water) = 1.05 + 0.013 + 10 = 11m.
(13)
Hemal said:
7 years ago
Please describe the solution.
(1)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers