IndiaBIX

Aptitude - Surds and Indices

Exercise : Surds and Indices - General Questions
11.
(243)n/5 x 32n + 1 = ?

9n x 3n - 1
1
2
9
3n
Answer: Option
Explanation:

Given Expression
= (243)(n/5) x 32n + 1

9n x 3n - 1
= (35)(n/5) x 32n + 1

(32)n x 3n - 1
= (35 x (n/5) x 32n + 1)

(32n x 3n - 1)
= 3n x 32n + 1

32n x 3n - 1
= 3(n + 2n + 1)

3(2n + n - 1)
=

33n + 1

33n - 1
= 3(3n + 1 - 3n + 1)   = 32   = 9.

12.
1 + 1 = ?
1 + a(n - m) 1 + a(m - n)
0
1
2
1
am + n
Answer: Option
Explanation:

1 + 1 =
1  +  1
1 + an
am
1 + am
an
1 + a(n - m) 1 + a(m - n)

   = am + an
(am + an) (am + an)

   = (am + an)
(am + an)

   = 1.

13.
If m and n are whole numbers such that mn = 121, the value of (m - 1)n + 1 is:
1
10
121
1000
Answer: Option
Explanation:

We know that 112 = 121.

Putting m = 11 and n = 2, we get:

(m - 1)n + 1 = (11 - 1)(2 + 1) = 103 = 1000.

14.
xb (b + c - a) . xc (c + a - b) . xa (a + b - c) = ?
xc xa xb
xabc
1
xab + bc + ca
xa + b + c
Answer: Option
Explanation:
Given Exp.
= x(b - c)(b + c - a) . x(c - a)(c + a - b) . x(a - b)(a + b - c)
= x(b - c)(b + c) - a(b - c)  .  x(c - a)(c + a) - b(c - a)
   .  x(a - b)(a + b) - c(a - b)
= x(b2 - c2 + c2 - a2 + a2 - b2)  .   x-a(b - c) - b(c - a) - c(a - b)
= (x0 x x0)
= (1 x 1) = 1.
15.
If x = 3 + 22, then the value of x - 1 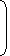is:
x
1
2
22
33
Answer: Option
Explanation:

x - 1 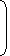2 = x + 1 - 2
x x

   = (3 + 22) + 1 - 2
(3 + 22)

   = (3 + 22) + 1 x (3 - 22) - 2
(3 + 22) (3 - 22)

   = (3 + 22) + (3 - 22) - 2

   = 4.

x - 1 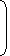= 2.
x

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers