Engineering Mechanics - General Principles - Discussion
Discussion Forum : General Principles - General Questions (Q.No. 6)
6.
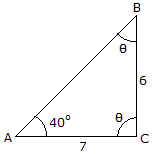
Determine the angles
 and
and  and the length of side AB of the triangle. Note that there are two possible answers to this question and we have provided only one of them as an answer.
and the length of side AB of the triangle. Note that there are two possible answers to this question and we have provided only one of them as an answer.Discussion:
17 comments Page 1 of 2.
Shubham said:
9 years ago
Guys here we can't use trigonometry relations.
Because one of them angle is not 90°.
Because one of them angle is not 90°.
Gaurav said:
9 years ago
I totally agree with you @Devendra, by using sin formula one can solve this problem in an accurate manner.
In triangle ABC, angle A is given 40, By applying the formula.
6/sin 40 = 7/sin B, we get sin B = 48.58.
Now the sum of all angles of triangle = 180.
We get angle C = 91.4.
Again 6/sin 40 = c/sin 91. 4, we get C = 9.33.
In triangle ABC, angle A is given 40, By applying the formula.
6/sin 40 = 7/sin B, we get sin B = 48.58.
Now the sum of all angles of triangle = 180.
We get angle C = 91.4.
Again 6/sin 40 = c/sin 91. 4, we get C = 9.33.
Devendra said:
1 decade ago
We can not use trigonometry or Pythagoras theorem unless we have right angle triangle, here the figure is seems to be right angle triangle but it is not.
So we can use sin formula a/sinA=b/sinB=c/sinC where a, b, c are the sides opposites to the angle A, B, C.
So we can use sin formula a/sinA=b/sinB=c/sinC where a, b, c are the sides opposites to the angle A, B, C.
Mannu kumar said:
1 decade ago
bc = 6, ac = 7 ab = ? now, trigonometric from ab^2 = bc^2+ac^2.
ab^2 = 36+49 = 9.21.
Answer = D.
ab^2 = 36+49 = 9.21.
Answer = D.
(1)
Manoranjan patra said:
1 decade ago
I think 1st we check about diagonal ,so according to pythagorean triangle formula. 6*2+7*2=h*2( * means power ) so h =9.22 , but if angle angle acb is 90. So then see the option, in option A and option D h=9.22, but in that 2 option angle acb not 90 degree.
Then in option C angle is 90 degree but diagonal h is not 9.22, so this is also incorrect. Because if angle is 90 then h must be 9.22.
So easily you without calculation you may find option D is. correct.... thanks.
Then in option C angle is 90 degree but diagonal h is not 9.22, so this is also incorrect. Because if angle is 90 then h must be 9.22.
So easily you without calculation you may find option D is. correct.... thanks.
Srikant said:
1 decade ago
Need to apply sin rule,
AB/sin(C) = BC/sin(A) = CA/sin(B)
IN THE PROBLEM,
AC=7, BC=6 AND ANGLE A=40 GIVEN
AB/sin(C) = 6/sin(40) = 7/sin(B).
sin(B) = [7*sin(40)]/6 from this we will get B angle.
Then C=180-A-B.
AFTER THAT AB = [6/sin(40)]*sin(C).
AB/sin(C) = BC/sin(A) = CA/sin(B)
IN THE PROBLEM,
AC=7, BC=6 AND ANGLE A=40 GIVEN
AB/sin(C) = 6/sin(40) = 7/sin(B).
sin(B) = [7*sin(40)]/6 from this we will get B angle.
Then C=180-A-B.
AFTER THAT AB = [6/sin(40)]*sin(C).
Ammu said:
1 decade ago
Why cant we use cos40=7/AB=>AB=9.14 directly......it is also correct method.
Sujit kumar singh said:
1 decade ago
See you are right but sin(theta) is also used for side and angle relation.
Like formula is a/sin(alpha)=b/sin(bita)=c/sin(gama).
Where a,b,c are the sides of triangle and alpha, bita,gama are the angle infront of side of triangle like a, b, c.
So we can solve as:
7/sin(fai)=6/sin(40)
so sin(fai)=0.7499
and fai=48.58 degree.
Also theta=180-(40+48.58)=91.42 degree.
And using same formula as above we can find length AB as
6/sin(40)=AB/sin(91.42)
so AB=9.33
Like formula is a/sin(alpha)=b/sin(bita)=c/sin(gama).
Where a,b,c are the sides of triangle and alpha, bita,gama are the angle infront of side of triangle like a, b, c.
So we can solve as:
7/sin(fai)=6/sin(40)
so sin(fai)=0.7499
and fai=48.58 degree.
Also theta=180-(40+48.58)=91.42 degree.
And using same formula as above we can find length AB as
6/sin(40)=AB/sin(91.42)
so AB=9.33
PRAMOD said:
1 decade ago
COS40=7/AB
AB=7/COS40
AB=9.13
AB=7/COS40
AB=9.13
Kcrkr said:
1 decade ago
Please let me know why you are using Sin theta, I think sin is using against for length / hypotenus, we get for cos theta also because we know base of triangle. Then answer is 9.22.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers