Mechanical Engineering - Theory of machines - Discussion
Discussion Forum : Theory of machines - Section 9 (Q.No. 13)
13.
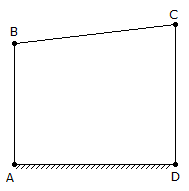
ABCD is a four bar mechanism in which AB = 310 mm and CD = 450 mm. AB and CD are both perpendicular to the fixed link AD, as shown in the below figure. If the velocity of B at this condition is v. Then the velocity of C is

Discussion:
20 comments Page 2 of 2.
Manish said:
6 years ago
A is the correct option. I too agree.
Parashuram said:
6 years ago
At this condition velocity of B is equals to the velocity of C, because at this instant instantaneous center be lie at infinity otherwise velocity of B is not equal to the velocity of C.
Shrivardhan said:
6 years ago
A is correct answer as per ACE notes.
Anuj said:
6 years ago
A is the correct answer. I too agree.
Kiran said:
8 years ago
Option A is the correct answer. Since crank and rocker are parallel to each other the coupler angular velocity becomes zero. So, Vb=Vc.
Ramesh said:
8 years ago
Yes, A is the correct answer.
Kais said:
8 years ago
I believe A is the correct answer as both vB and Vc are horizontal and link BC can not be rotating so has no contribution to the velocity of vC/A; That is, w3 = 0 (or VCA=0). You may also use instantaneous center I24 and find the relationship between w2 and w4, they are proportional with w2/w4=CD/AB so vB=Vc.
JKVERMA37 said:
9 years ago
A is right option, because in condition link BC is in pure translation.
Som said:
9 years ago
{45 ÷ 31} * v = (3/2)v.
Abhi said:
10 years ago
I think the answer is A, as we draw a velocity diagram it will be a straight line, where B nd C coincide. So, Vb = Vc.
I have a question @G Nagaraju.
Why have you taken the angular velocity of both same?
I have a question @G Nagaraju.
Why have you taken the angular velocity of both same?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers
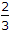 v
v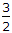 v
v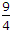 v
v