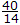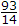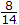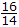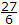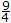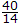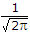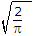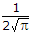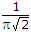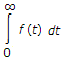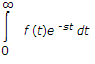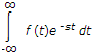Electronics and Communication Engineering - Signals and Systems
Exercise : Signals and Systems - Section 3
- Signals and Systems - Section 1
- Signals and Systems - Section 2
- Signals and Systems - Section 3
- Signals and Systems - Section 4
- Signals and Systems - Section 5
- Signals and Systems - Section 6
- Signals and Systems - Section 7
- Signals and Systems - Section 8
- Signals and Systems - Section 9
- Signals and Systems - Section 10
46.
If f(t) = - f(- t) satisfies Drichlet conditions, then f(t) can be expanded in Fourier series containing
Answer: Option
Explanation:
Since f( - t) = - f(t) only sine terms will be present because sin (- x) = - sin x.
47.
The joint probability function of two discrete random variable X and Y is given by
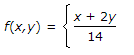x = 0, 2, y = 2, 3 then E(y) is
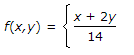x = 0, 2, y = 2, 3 then E(y) is
Answer: Option
Explanation:
.
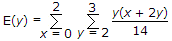
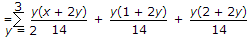
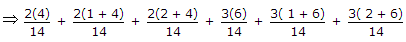
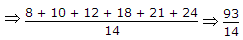48.
The joint probability function of two discrete random variable X and Y is given by
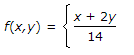x = 0, 2, y = 2, 3 variance σ2 will be
[Hint: σ2 = E(X2) - μ2 ⇒ E(X2) - (E(X))2]
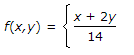x = 0, 2, y = 2, 3 variance σ2 will be[Hint: σ2 = E(X2) - μ2 ⇒ E(X2) - (E(X))2]
zero
Answer: Option
Explanation:
.
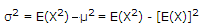
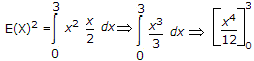
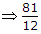
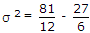
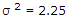49.
A probability density function is given by p(x) = Ke-x2/2 for -∞ < x < ∞ , The value of K should be
Answer: Option
Explanation:
K can be found by integrating and equating the area under the curve equal to 1.
50.
The Laplace transform of f(t) is
none of the above
Answer: Option
Explanation:
£f(t) =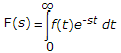 
£-1F(s) = f(t)
£[a f1(t) + bf2(t)] = aF1(s) + bF2(s)
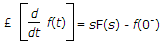
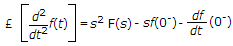
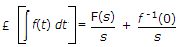
where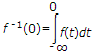 
£[f(t - T)] = e-sT F(s)
£[e-at f(t)] = F(s + a)
Initial value theorem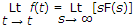 
Final value theroem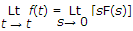 
Convolution Integral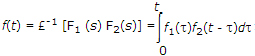 
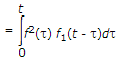
where t is dummy variable for t.
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers